https://doi.org/10.22267/rceilat.225051.104
ARTÍCULO DE INVESTIGACIÓN
Diseño de una estrategia
didáctica basada en la simbología Pasto para desarrollar el pensamiento
geométrico
Design of a didactic strategy based on Pasto symbology to develop geometric thinking
Martin Favian
Coral Parra
Magíster en Educación - Corporación
Universitaria Iberoamericana
Email: martinparra12@gmail.com
Carlos Henry Sandoval
Magíster en la Gestión de la Tecnología en
la Educación - Corporación Universitaria Iberoamericana
Email: carlos.sandoval@ibero.edu.co
Magaly Andrea Argoty
Cantincus
Magíster en Educación - Corporación
Universitaria Iberoamericana
Email: magali.andrea@hotmail.com
Adriana Del Carmen Mejía Romo
Magíster en Educación - Corporación
Universitaria Iberoamericana
Email: amejiar1@ibero.edu.co
Recibido: 20/08/2021, Aprobado: 9/11/2022
Resumen
El entorno que rodea a los niños y las niñas está
lleno de formas geométricas, por esta razón, saber distribuir los objetos en el
espacio es una de las tantas razones de la enseñanza de la geometría en los
escenarios escolares. La presente investigación se enmarca en el desarrollo del
pensamiento geométrico, y tiene como objetivo el diseñar el planteamiento de
una estrategia didáctica que permita a los estudiantes de grado quinto de la
Institución Educativa Agroindustrial Los Pastos el fortalecimiento de los
procesos geométricos a partir de elementos simbólicos propios de su cultura.
Para esto, se utiliza el estudio y la aplicación
del Modelo de Razonamiento Geométrico de Van Hiele, buscando facilitar una
mejor comprensión y aplicación de la geometría. El diseño metodológico en el cual
se fundamenta esta investigación es de tipo descriptivo e interpretativo. Los
instrumentos empleados para la recolección de la información fueron el
cuestionario, que permitió identificar las causas de las dificultades en el
aprendizaje del proceso geométrico y la entrevista semiestructurada para poder
responder a las necesidades individuales y colectivas planteadas por los investigadores. El
grupo focal fue el grado quinto de básica primaria de la Institución Educativa
Agroindustrial Los Pastos. Por último, se concluye que el planteamiento de la
estrategia didáctica pretende generar un cambio en la práctica metodológica del
docente impactando en los procesos de enseñanza y aprendizaje significativo en
la población objeto del estudio.
Palabras
claves: Aprendizaje
Significativo, enseñanza-aprendizaje, estrategia didáctica, pensamiento
geométrico
Abstract
The environment that surrounds children is full of
geometric shapes, for this reason, knowing how to distribute objects in space
is one of the many reasons for teaching geometry in school settings. This
research is part of the development of geometric thinking, and its objective is
to design the approach of a didactic strategy that allows fifth grade students
of the Agroindustrial Educational Institution the Pasto’s to strengthen geometric processes based on symbolic
elements. specific to their culture.
For this, the study and application of the Van Hiele Geometric Reasoning Model is used,
seeking to facilitate a better understanding and application of geometry. The
methodological design on which this research is based
is descriptive and interpretive. The instruments used to collect the
information was the questionnaire, which made it possible to identify the
causes of the difficulties in learning the geometric process and the
semi-structured interview to be able to respond to the individual and
collective needs raised by the researchers. The focus group was the fifth grade
of elementary school from the Pasto’s Agroindustrial
Educational Institution. Finally, it is concluded that the approach of the
didactic strategy aims to generate a change in the methodological practice of
the teacher, impacting on the teaching and significant
learning processes in the population under study.
Keywords: meaningful
learning, teaching-learning, didactic strategy, geometric thinking.
Introducción
De acuerdo con la definición de los estándares básicos de competencias en matemáticas, el pensamiento geométrico hace referencia al conjunto de los procesos cognitivos a través de los cuales se construyen y se manipulan las representaciones mentales de los objetos relacionados con el espacio, sus transformaciones, y sus diversas traducciones o representaciones materiales, además contemplan las actuaciones del sujeto en todas sus dimensiones, con el fin de interactuar de diferentes maneras con los objetos, desarrollar variadas representaciones y, a través de la coordinación entre ellas, hacer acercamientos conceptuales que beneficien la creación y asimilación de nuevas representaciones mentales.
Esta
investigación se realiza con el propósito de despertar en el estudiante el
interés por aprender la geometría a través de la simbología de la Cultura Pasto
(Sol de los Pastos, Churo Cósmico, Danzantes, Chamanes, Machines), dicha
propuesta es innovadora porque cambia el escenario de aprendizaje en el cual
los estudiantes están habituados a trabajar, ya que la propuesta está
relacionada directamente con la manipulación de material concreto, colorido y
liviano, escogido según su predilección, sin la necesidad de utilizar elementos
escolares tradicionales, evitando así permanecer quietos y sin la oportunidad
de expresar su punto de vista frente a la problemática.
Además,
se enmarca en el desarrollo del pensamiento geométrico, donde permite a los
estudiantes de grado quinto de la Institución Educativa Agroindustrial Los
Pastos, la identificación de procesos de asimilación y aplicación de la
geometría, para ello se toma como base fundamental elementos propios de su
comunidad (figuras o representaciones graficas las cuales poseen diferentes
significados) rescatando valores culturales de la etnia de los pastos como el
trabajo colaborativo o la minga de pensamiento (lluvia de ideas).
Esta
propuesta surge a raíz de los vacíos conceptuales y dificultades en la aplicación
de las diferentes competencias de esta rama de las matemáticas, al igual que
los resultados en las distintas pruebas (externas e internas), ya que la mayoría
registra un nivel bajo y/o inferior. Por esta razón se pensó en diseñar una
estrategia didáctica que permita el desarrollo del pensamiento geométrico a
través de la simbología de Los Pastos y que genere aprendizaje significativo, el
cual contribuirá a mejorar en alto porcentaje los vacíos conceptuales que presentan
los estudiantes.
A
su vez, con esta propuesta se pretende dar una alternativa de solución a uno de
los problemas que se han presentado durante varios años en la institución con
relación a la enseñanza-aprendizaje de la geometría, de igual manera se trata
de incitar a los docentes de matemáticas a innovar su práctica docente; de ahí
que esta investigación puede ser uno de los caminos para que los estudiantes
desarrollen y apliquen habilidades y competencias correctamente dentro de
diferentes escenarios y que se pueden solucionar a través de aplicación del
pensamiento geométrico. Por tal razón, se hace necesario diseñar una estrategia
didáctica que sea valiosa e innovadora y que se convierta en el motor de
motivación estudiantil para participar e intervenir en los espacios de
formación mientras construyen aprendizajes significativos.
Antecedentes
La
geometría es la parte más concreta de las matemáticas, intuitiva y ligada a la
realidad, la cual ha sido estudiada alrededor de más de dos mil años, en niveles
crecientes de rigor, abstracción y generalidad. Existen conceptos básicos de
formas y de ubicación espacial los cuales se aprenden desde la infancia, esto
acompañado con la ayuda de los padres de familia y del contexto que los rodea.
Hubo un momento histórico en el que, al surgir las nuevas matemáticas en el
país durante los años 60, la geometría quedó relegada en los currículos de
matemáticas. Pero ante esta situación, en los años 70 surgió el modelo
denominado “enfoque de sistemas”, el cual propone dirigir los aspectos de las
matemáticas como sistemas y no como conjuntos, permitiendo que la geometría
haga parte nuevamente del currículo de matemáticas.
Por
tal razón es necesario construir una concepción elemental, en donde los niños
aprendan el concepto de estar atrás, adelante, arriba y abajo; e identificar
las figuras geométricas básicas como el cuadrado, el círculo y el triángulo (Schulmaister, 2008). Por otro lado, son variados los
estudios que demuestran a través del modelo de Van Hiele los problemas
cotidianos que se presentan en el escenario de las matemáticas y en particular
en geometría. A su vez, Hans Freudenthal, profesor de
Van Hiele llamó la atención de estos estudios, en su libro “Las matemáticas como
una obra educacional” (1973).
Igualmente,
Joanne Mayberry (Georgia College)
realizó la investigación sobre “Los niveles de pensamiento geométrico en
estudiantes para profesor”, y que según el modelo de Van Hiele demuestra que
los alumnos no estaban preparados para un curso formal de geometría deductiva,
pues se encontraban en niveles diferentes para distintos conceptos. Dentro de sus
conclusiones, se establece que desarrollar procedimientos de evaluación adecuados
puede ser un componente importante de la investigación.
Por
otra parte, Jaime Gutiérrez en Proceedings of de 11th
Internacional Conference of de PME vol. 3 (pp131-137)
un estudio de las características de los niveles de Van Hiele, en Bergeron, J.C. Herscovics, N. Kieran C. (1987), presentó las siguientes conclusiones de
su trabajo: en la primera, los niveles de 1 a 4 tienen estructura jerárquica. No
ocurre lo mismo con el 5º nivel. Por lo tanto, el modelo de Van Hiele es más
coherente si se elimina el 5. Así mismo, en la segunda conclusión, los niveles
de Van Hiele no tienen carácter global. Esta experiencia la realizó a 563 estudiantes
de la Escuela del Magisterio de la Universidad de Valencia. Por otra parte, la
doctora Adela Jaime de la Universidad de Valencia (1995) publica su artículo
¿Por qué los estudiantes no comprenden geometría? En este se muestra a través
de ejemplos, como los errores e incongruencias cometidas por los estudiantes,
se encuentran en una incomprensión entre docente y el estudiante, los cuales
hablan y razonan en diferentes niveles.
Las
investigaciones antes expuestas, entregan orientaciones en la enseñanza de la
geometría al usar el modelo Van Hiele. Por consiguiente, desde la teoría
crítica que orienta esta investigación, es necesario tener presente los requisitos
que la sustentan, los elementos que favorecen el deseo de cambio en los
docentes, y el avance del aprendizaje geométrico. De ahí que para lograr
cualquier cambio importante en la enseñanza-aprendizaje del estudiante, no sólo
reside en los contenidos o en el nuevo modelo de aprendizaje, sino también en
la estrategia metodológica del docente que subyace a la concepción de enseñanza
de calidad. El docente debe promover un espacio o un escenario concreto donde
el actúa pedagógicamente. Para ello se requiere que emita juicios en la toma de
decisiones de acuerdo con los cambios que se producen en el proceso de
aprendizaje, de igual manera debe ser capaz de construir sus propios materiales,
seleccionarlos o adecuarlos a la realidad y el contexto de sus estudiantes.
Por
otra parte, a nivel nacional se le ha dado prioridad a los diferentes estudios relacionados
con el pensamiento geométrico, en lo cual cabe mencionar el estudio
“Estrategias didácticas para fortalecer el pensamiento geométrico en estudiantes
de grado sexto” realizado por Dora Fanny Marín Grajales de la Universidad
Católica de Manizales, en 2013, quien plantea la necesidad de crear estrategias
didácticas para el aprendizaje de la geometría en estudiantes de grado sexto de
la Institución Educativa El Madroño del municipio de Belalcázar,
Caldas, estrategias que tienen por objetivo el ofrecer acciones pedagógicas
pertinentes que conduzcan a la formación de conocimientos, habilidades,
destrezas y aptitudes de los estudiantes, logrando el mejoramiento en los
procesos de enseñanza aprendizaje, favoreciendo a través de diferentes
actividades didácticas el trabajo personalizado por medio de talleres
individuales y grupales generando un desarrollo adecuado de pensamiento
geométrico.
También
cabe mencionar la investigación llamada “El Desarrollo del pensamiento
geométrico a partir del uso de estrategias didácticas soportadas en
herramientas computacionales y el modelo de Van Hiele” realizado por Eugenio Therán Palacio y Elver Oviedo Vergara,
ambos autores, magísteres en Educación de la Universidad de Sucre en 2018,
soportando su trabajo en la necesidad de fortalecer las competencias de los
docentes del área de matemáticas, y en especial de la geometría, de tal manera,
que se pueda evidenciar innovación en las prácticas pedagógicas y en el empleo
de metodologías que apuntan estratégicamente hacia el logro de un mejor
desempeño de los estudiantes, despertando en ellos el interés por aprender los
contenidos geométricos partiendo de situaciones cotidianas puestas en escena en
el aula de clase.
Y
por último, a nivel regional, el estudio “Urdiendo los saberes propios desde la
geometría sagrada del Pueblo Pasto” de la Universidad Nacional Abierta y a
Distancia (UNAD), en 2019, aludiendo a la geometría y simbología sagrada como
una manera de dar a conocer una idea, un saber, una acción y dar representación
a los contextos naturales, espirituales y sociales, de ahí que dentro de
urdiendo los saberes, se pretende que los niños y niñas reconozcan el tejido en
guanga como un medio para conocer y preservar la cultura e interaccionar con el
otro, despertando en cada uno de ellos la capacidad de asombro. Entre las
figuras geométricas que se retomarán en el proceso se encuentran, el sol de los
pastos, la espiral o churo cósmico, los monos, los machines y la wiphala como símbolo de identidad, político y social de las
comunidades indígenas, implementando y desarrollando proyectos encaminados al
rescate de los valores étnicos, culturales, artísticos y artesanales.
Metodología
El
diseño metodológico propuesto para esta investigación es de tipo descriptivo e
interpretativo, con un enfoque cualitativo, ya que los docentes interactúan con
los estudiantes a través de mingas de pensamiento buscando solucionar el
problema que presentan los niños y niñas del grado quinto, como lo afirma
Hernández-Sampieri, (2019) “el enfoque cualitativo
puede concebirse como un conjunto de prácticas interpretativas que hacen al
mundo “visible”, lo transforman y convierten en una serie de representaciones
en forma de observaciones, anotaciones, grabaciones y documentos”.
Por
otro lado, el enfoque interpretativo simbólico encuentra su génesis, en sus
diversas vertientes en el idealismo alemán, particularmente en Kant, quien
argumentó que la “realidad social existe en la idea antes que en los hechos
concretos” (Burrell & Morgan, 1979; Putnam, 1983,
p. 32). El tipo de conocimiento que se obtiene de la investigación interpretativa
es un conocimiento comprensivo, no prescriptivo, “se trata de comprender los
fenómenos educativos tal y como se producen en la práctica. Por tanto, es un
tipo distinto al conocimiento denominado científico: no trata de obtener leyes
ni regularidades en educación” (ScarbaTh, 1984, p.
123).
En
los trabajos de investigación científica, se utilizan distintos instrumentos para
la recopilación de datos; así pues, los instrumentos empleados en este trabajo
fueron el cuestionario, que permitió identificar las causas de las dificultades
en el aprendizaje del proceso geométrico, en palabras de García, F. et al.
(2006) “la recogida de información es una parte crucial de una investigación,
ya que, cuanto más clara esté, menos laborioso será el desarrollo de un
estudio”; para Hernández-Sampieri et al. (2008)
“los cuestionarios consisten en una serie de preguntas abiertas y/o cerradas
respecto de una o más variables a medir y son probablemente el instrumento más utilizado
para recolectar datos”. Asimismo, se empleó como instrumento de recolección de
la información la entrevista semiestructurada, con el fin de poder responder a
las necesidades individuales y colectivas planteadas por los investigadores. En
palabras de Troncoso, C. y Amaya-Placencia, A. (2017)
quienes manifiestan que “una entrevista bien formulada permite un acercamiento
a poblaciones, mientras que otras técnicas dejarían contenido importante por
fuera” (p. 3). Al mismo tiempo se trabajó con el grupo focal del grado quinto
de básica primaria de la Institución Educativa Agroindustrial Los Pastos.
Ahora
bien, dentro de esta investigación se propone tres acciones principales, como
primer momento la aplicación del instrumento de la prueba diagnóstica, que
permitirá identificar falencias que presentan los estudiantes de grado quinto
en el área de geometría, como segundo momento, se tiene una entrevista
semiestructurada a los docentes de la Institución, que han laborado en los
últimos seis años en este grado, esto con el fin de realizar un diagnóstico
sobre el desarrollo del pensamiento geométrico y en la última fase del segundo
momento, se realizará la entrevista semiestructurada al gobernador indígena
como autoridad dentro del resguardo, quien logrará contribuir con conocimientos
acerca
de
la simbología y la Cultura Pasto. Y, como tercer momento, el diseño de la estrategia
didáctica por parte de los investigadores, con la cual se pretenderá desarrollar
el pensamiento geométrico reforzando conceptos básicos de dicho conocimiento, a
través de la simbología de la cultura Pasto. Por otro lado cabe aclarar que la
población objeto de estudio de la propuesta de esta investigación está
conformada por: el gobernador indígena como autoridad dentro del resguardo, los
docentes y los estudiantes del grado quinto de básica primaria de la
Institución, de ahí que para el desarrollo y ejecución de esta propuesta de la
investigación se tomó una muestra que en el proceso cualitativo y según
Hernández et al. (2008), “es un grupo de personas, eventos, sucesos,
comunidades, etc. sobre el cual se habrán de recolectar los datos, sin que
necesariamente sea representativo del universo o población que se estudia” (p.
562).
Tabla
1. Población encuestada para el objeto del estudio.
|
Estratos |
Población Total |
|
Estudiantes grado
quinto |
16 |
|
Profesores grado
quinto |
6 |
|
Líder comunitario |
1 |
|
TOTAL |
23 |
Nota:
Se muestra el total de los participantes en la
investigación.
Fuente: elaboración propia.
Resultados
Según
la prueba diagnóstica realizada a los estudiantes de grado quinto y teniendo en
cuenta el modelo de Van Hiele, se puede analizar que, al desarrollar preguntas
concernientes al nivel 0 los estudiantes aprueban de manera satisfactoria o
alcanzan el nivel sin ningún problema, lo que quiere decir que los niños
visualizan correctamente las diferentes figuras geométricas por su forma como
un todo, y las descripciones que realizan son visuales comparándolas a su vez
con elementos familiares de su entorno, por lo tanto los niños y niñas no
presentan ninguna dificultad al desarrollar este nivel.
Con
respecto a las preguntas y temáticas del Nivel 1, se observa que hay cierta
dificultad en la identificación de las propiedades de las diferentes figuras geométricas,
poniendo en evidencia la falta de comprensión y análisis de la materia. De
igual modo, dentro del nivel dos, los estudiantes pueden describir las figuras,
pero no las relacionan ni identifican todas sus propiedades; tampoco logran
realizar clasificaciones de objetos y figuras geométricas. Según esto se puede
inferir que existe falta de comprensión en el lenguaje geométrico, por lo
tanto, se deduce que se debe mejorar los procesos de comprensión lectora.
De
la misma manera se observa que hay dificultad en solucionar y plantear problemas
geométricos, es decir, no logran identificar las condiciones necesarias y
suficientes para cumplir con la tarea. Por lo anterior se debe trabajar y reforzar
los procesos mentales en cuanto se refiere al empleo de operaciones y propiedades
geométricas básicas.
En
cuanto a la entrevista de los estudiantes, y los comentarios aportados por
ellos, se puede deducir el papel fundamental que cumple el profesor en la
motivación dentro del proceso de enseñanza-aprendizaje, porque con este se
logra asimilar fácilmente las temáticas abordadas dentro del aula, sin embargo,
se debe reconocer que no todos los estudiantes avanzan al mismo ritmo y por
tanto se requiere de un constante seguimiento a aquellos que presentan mayor
dificultad al desarrollar los contenidos. Al hacer alusión al pensamiento
geométrico, los estudiantes afirman que la resolución de problemas geométricos
se convierte en un reto para solucionarlos, por tanto, los docentes de
matemáticas deben contar con amplia base de conocimientos que les permitan
guiar con mayor facilidad, buen criterio y mayores posibilidades de desarrollo.
Del
mismo modo en la entrevista a profesores, se observa que es de suma importancia
lograr que el estudiante se interese por aprender, porque quizá esa sea la
única manera de adquirir nuevos conocimientos duraderos, para ello se debe
realizar una retroalimentación permanente con el único propósito de alcanzar
los objetivos propuestos dentro de la asignatura.
En
cuanto a la entrevista al director de grupo, recalca la importancia que se debe
dar a los estudiantes con dificultades; de ahí el papel fundamental que juegan
las diferentes estrategias pedagógicas implementadas para abordar un tema
específico. Según esto, se hace necesario una propuesta innovadora que genere
un cambio en la práctica de aula, un clima de mayor atención, participación y receptividad
hacía los nuevos conocimientos, teniendo en cuenta que el modelo de Van Hiele,
se desarrolla de una manera secuencial donde cada nivel es la base del
siguiente y está caracterizado por un lenguaje particular, símbolos y métodos
de inferencia específicos. De acuerdo con lo anterior se hizo necesario
plantear y diseñar una unidad didáctica para favorecer el proceso enseñanza
aprendizaje del pensamiento geométrico a través de la simbología de los Pastos,
con los estudiantes de grado quinto, evidenciando el siguiente resultado: Propuesta
del diseño de la estrategia pedagógica.
En
la cultura ancestral de la etnia de los Pastos en el municipio de Ipiales, existen
comunidades indígenas en donde hasta la actualidad se ponen en práctica los
usos y costumbres heredados de los mayores a los renacientes y sus
generaciones. De allí la importancia de conocer a través del diseño de esta
unidad didáctica conceptos o definiciones de algunas representaciones de la
Simbología del Pueblo Pasto que sirven de apoyo pedagógico en el pensamiento
geométrico.
La
propuesta de la unidad didáctica es una forma de organizar conocimientos y
experiencias que considera la diversidad de elementos que contextualizan el
proceso (nivel de desarrollo del estudiante, medio sociocultural y familiar,
proyecto curricular y recursos disponibles) para “regular la práctica de los
contenidos, seleccionar los objetivos básicos que pretende conseguir, las
pautas metodológicas con las que trabajará y las experiencias de enseñanza-aprendizaje
necesarias para perfeccionar dicho proceso” (Gallego, 2007, p. 4).
De
ahí que esta se empleará como herramienta pedagógica para los docentes de la
básica primaria de grado quinto con el propósito de promover aprendizaje significativo
en el pensamiento geométrico, lo cual permitirá afianzar los procesos de
enseñanza-aprendizaje de manera estructurada, planeada, y metódica a través de
diferentes actividades, tomando como referente elementos de su contexto o
culturales como la simbología de los Pastos.
Esta
propuesta nace como una alternativa pedagógica a raíz de los bajos resultados
obtenidos en las diferentes pruebas internas elaboradas por los docentes de la
institución y las externas como Saber 5°
la
cual es organizada por el Icfes con el aval del
Ministerio de Educación Nacional. Además, desde el año 2015, los resultados de
las pruebas Saber configuran dos de los cuatro componentes evaluativos del
Índice Sintético de Calidad Educativa (ISCE), una métrica diseñada por el mismo
Ministerio de Educación Nacional, MEN, para analizar el desempeño educativo de
los colegios.
Con
base a lo anterior, los resultados obtenidos en los últimos años en estas pruebas,
los niños y niñas presentan dificultades en el área de matemáticas, específicamente
en el pensamiento geométrico, según los estándares básicos de competencias
relacionan el estudio de la geometría con el arte y la decoración, con el
diseño y construcción de diseños artesanales y tecnológicos, con la educación
física, los deportes y la danza, con la observación y la reproducción de
patrones (Nacional, 2006). En concordancia con lo anterior, se hace necesario
trabajar con estrategias didácticas diferenciales encaminadas a fortalecer sus
conocimientos universales de forma transversal con la cultura de los Pastos.
Hay
que mencionar, que en esta propuesta didáctica, se toma como pretexto elementos
culturales y simbología de la etnia del resguardo indígena de Ipiales, para
llegar a cumplir con el objetivo de fortalecer los conocimientos y obtener un
aprendizaje significativo que permitirá mejorar los procesos de la enseñanza
aprendizaje del pensamiento geométrico, al mismo tiempo, se empleará una
metodología colaborativa en la cual participan estudiantes, padres de familia y
docentes haciendo una triangulación de saberes a partir del contexto indígena.
Ahora bien teniendo en cuenta que en el área de matemáticas
existen cinco pensamientos establecidos por el MEN, en sus estándares básicos
de competencias, los cuales son de carácter obligatorio abordarlos, por tanto,
el número de horas semanales para la aplicación de esta unidad didáctica será
de dos horas, con el fin de trabajar simultáneamente los demás pensamientos que
son de gran importancia y se integran para ampliar los conocimientos
matemáticos.
Figura 1. El sol de los pastos en el
plano cartesiano.
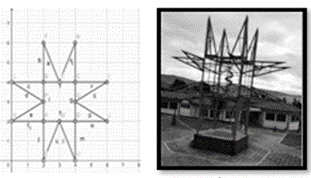
Nota:
Imagen elaborada en programa en línea.
Fuente:
https://www.geogebra.org/classic?lang=es
En
la unidad didáctica se pretende trabajar la importancia de la geometría desde
tiempos remotos, el legado que dejaron los antepasados con sus conocimientos empíricos
a través de la experiencia y como plasmaron su teoría geométrica en el mundo,
asimismo los elementos relacionados con las figuras, características y
clasificación en donde la temática a abordar será transversal, la cual presenta
gráficas con elementos geométricos y de igual forma la infraestructura de la
Institución servirá como apoyo temático debido a su forma hexagonal denominada
bohíos (referencia a la vivienda ancestral del pueblo Pasto).
Inicialmente,
el docente trabajará la unidad didáctica diseñada a partir de situaciones
prácticas, las cuales pueden ser relacionadas con el contexto cotidiano de los
estudiantes, se plantea una situación problema con figuras geométricas donde el
uso del plano cartesiano permita resolver la situación planteada inicialmente,
los estudiantes desarrollarán la actividad propuesta de manera grupal para
favorecer los distintos puntos de vista, a partir de las indicaciones dadas por
el profesor, la ubicación de pares ordenados e invita a la creación de
representaciones de la simbología Pasto de una manera didáctica.
Figura 2. Representación
del Machín (mono) simbología Pasto.
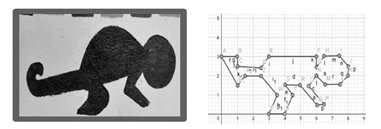
Plano
cartesiano: ubicando pares ordenados, trabajo realizado por estudiante del
grado quinto.
Fuente:
Elaboración propia.
De
igual forma, la unidad didáctica, también ofrece actividades pedagógicas dirigidas
y orientadas a fortalecer la temática de los ángulos, por ejemplo, definición,
clasificación y medición, se trabaja de forma práctica y contextualizada con
espacios y figuras representativas de la cultura de los Pastos. Además, se
aborda las características de las figuras geométricas, polígonos que se
identifican en las representaciones ancestrales que inducen a la producción y
elaboración de una artesanía cultural aplicando la técnica del tejido de
pulseras o pectorales con pepas de mostacilla en donde se plasman formas geométricas
para construir un arte con simbología Pasto.
Figura
3. Cerámica
Pasto
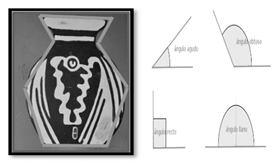
Nota:
Fotografía tomada en la Institución Educativa Agroindustrial Los Pastos.
Fuente:
Elaboración propia.
Además, es importante resaltar que la propuesta de esta unidad
didáctica es el fortalecimiento del pensamiento geométrico junto a la identidad
cultural de los estudiantes, al mismo tiempo motivando a trabajar los
diferentes escenarios pedagógicos, culturales y étnicos para que los
aprendizajes sean significativos al momento de desarrollar las actividades
planteadas por el docente.
Figura
4. Simbología
Ancestral

Nota:
Fotografía tomada de la I.E.A. Los Pastos y trabajo realizado por estudiantes
del grado quinto.
Fuente:
Elaboración propia.
Conclusiones
Con
el desarrollo de este trabajo se pretende generar un cambio en la práctica
docente, mejorando el ambiente de aprendizaje, logrando mayor atención, interés
y participación por parte del estudiante. Además, fortalece el trabajo
colaborativo, permitiéndoles a los estudiantes apoyarse entre ellos y construir
sus propios conocimientos bajo la orientación y supervisión del docente.
La
unidad didáctica a la que hace mención la presente investigación realiza un
aporte valioso por su elaboración, partiendo de una planeación detallada en
cada componente teniendo en cuenta los lineamientos básicos propuestos por el
MEN. La trasposición didáctica del conocimiento es estructurada, planificada y
diseñada para cada momento de la clase, con videos, talleres, actividades
evaluativas, entre otras, donde cada una de ellas ha pasado por un filtro de
planeación para construir y más adelante aplicar.
Con
este proyecto de investigación se quiere promover líneas de trabajo futuras
para lograr que este sea un referente en el área de matemáticas, de ahí la
importancia que adquieren las formas geométricas de la simbología Pasto para
potenciar el pensamiento geométrico, y con ello se convierta en el inicio para
futuras investigaciones relacionadas con el desarrollo de este pensamiento y
avanzar hacia nuevas estrategias didácticas que permitan a los estudiantes
alcanzar un aprendizaje significativo y éste se mire reflejado de manera
positiva en las diferentes pruebas.
Así
mismo se quiere mejorar los resultados por parte de los estudiantes en las
pruebas Saber de grado 5°, y de esta manera la Institución Educativa Agroindustrial
Los Pastos pueda ser reconocida como la Institución pionera en la
implementación de nuevas metodologías pedagógicas buscando potenciar el
pensamiento geométrico.
Otro
punto que se debe destacar de esta estrategia es el empleo de elementos
culturales en el desarrollo del pensamiento geométrico teniendo como punto de
confluencia la tradición y simbología Pasto a través del estudio de diferentes
figuras geométricas y las temáticas de la materia, de igual forma esto les
permitirá a los estudiantes apropiarse de su idiosincrasia como indígenas.
Declaración
Reconocimiento
a la Universidad Corporación Universitaria Iberoamericana, Facultad de
Educación Posgrados - Maestría en Educación, a la Institución Educativa
Agroindustrial los Pastos, quien permitió realizar y aplicar la propuesta de
investigación, Directivas, docentes, padres de familia y en especial a los
estudiantes focalizados quienes participaron activamente y mostraron gran
interés, de igual forma al Mg. Carlos Henry Sandoval Bravo por su asesoramiento
en el proceso de elaboración de tesis - artículo.
Bibliografía
1. American Psychological Association (2020). Publication manual of the American Psychological Association
(7th ed.). https://doi.org/10.1037/0000165-
000
2.
Aroca,
A. (2014). La lógica de elaboración en los diseños de los platos de las
culturas
prehispánicas
de Nariño. Actualidad
& Divulgación Científica, pp. 587-596. http://www.scielo.org.co/pdf/rudca/v17n2/v17n2a30.pdf
3.
Aroca, A. (2007). Una
propuesta de enseñanza de geometría desde una perspectiva cultural. Tesis
de Grado en Maestría en Educación con Énfasis en Educación Matemática.
Universidad del Valle, Santiago de Cali. http://etnomatematica.org/articulos/Tesis_maestria_Aroca.pdf
4.
Aza,
D. (2016). Iconografía
Pastos un saber ancestral. Tesis de Grado. Universidad del
Valle, Santiago de Cali. https://bibliotecadigital.univalle.edu.co/handle/10893/17736
5.
Barriga,
F. (2002). Estrategias
docentes para un aprendizaje significativo. México: McGraw
Hill. https://buo.org.mx/assets/diaz-barriga%2C---estrategias-docentesparaun-aprendizaje-significativo.pdf
6.
Cáceres,
C. (2016). La sistematización de la unidad didáctica en educación ambiental: Una
aproximación desde la experiencia en la ruralidad. Educere, 249-257. https://www.redalyc.org/pdf/356/35649692006.pdf
7.
Circulo
Solar (3 de mayo de 2013). Obtenido de https://circulosolar.wordpress.com/2013/05/03/la-chakana/
8.
Chamorro,
M. (2005). Didáctica
de las Matemáticas para Educación Infantil. Madrid, España:
Pearson Educación. https://unmundodeoportunidadesblog.files.wordpress.com/2016/02/didactica-matematicas-en-infantil.pdf
9.
De
Bono, E. (1970). El
Pensamiento Lateral. Manual de creatividad. Buenos Aires,
Argentina: Editorial Paidós SAICF. https://tecnologia3bunlp.files.wordpress.com/2015/03/edward-de-bono-pensamiento-lateral.pdf
10.
Díaz,
F. & Rojas, G. (2002). “Estrategias docentes para un aprendizaje
significativo”: Una interpretación constructivista. México: McGraw Hill, pp.
231-249. https://buo.org.mx/assets/diaz-barriga%2C---estrategias-docentes-para-un-aprendizajesignificativo.pdf
11.
Fouz,
F. & Berritzegune, D. (2001). Modelo de Van Hiele
para la didáctica de la Geometría. Ataritzar Bidea. Donostia. http://www.xtec.cat/~rnolla/Sangaku/SangWEB/PDF/PG-04-05-fouz.pdf
12.
Gallego, D. (2007). Los estilos de aprendizaje y la
enseñanza de las matemáticas. Revista Complutense de
Educación, 95-112.
https://revistas.ucm.es/index.php/RCED/article/view/RCED0808120095A
13.
Jiménez,
A. & Robles, F. (2016). Las estrategias didácticas y su papel en el
desarrollo del proceso de enseñanza aprendizaje. Educateconciencia,
Vol.
9, No. 10. pp. 106-113. http://192.100.162.123:8080/bitstream/123456789/1439/1/Las%20estrategias%20didacticas%20y%20su%20papel%20en%20el%20desarrollo%20del%20proceso%20de%20ense%C3%B1anza%20aprendizaje.pdf
14.
Marín,
D. (2013). Estrategias
didácticas para fortalecer el pensamiento geométrico, en el grado sexto de la
Institución Educativa el Madroño de Belalcázar,
Caldas. Tesis
de Grado. Universidad Católica de Manizales. https://docplayer.es/22799296-Estrategias-didacticas-para-fortalecer-el-pensamiento-geometrico-en-estudiantesde-grado-sexto-dora-fanny-marin-grajales.html
15.
Ministerio
de Educación Nacional de Colombia (2006). Estándares
básicos de competencias en matemáticas. Potenciar el pensamiento matemático:
¡Un reto escolar!, pp.
46-89. https://www.mineducacion.gov.co/1621/articles-340021_recurso_1.pdf
16.
Ministerio
de Educación Nacional de Colombia (2006). Estándares
Básicos de Competencias en Lenguaje, Matemáticas, Ciencias y Ciudadanas. Guía
sobre lo que los estudiantes deben saber y saber hacer con lo que aprenden. Bogotá:
Ministerio de Educación Nacional. https://www.mineducacion.gov.co/1621/articles-340021_recurso_1.pdf
17.
Revelo,
O. Collazos, C. & Jiménez, J. El trabajo colaborativo como estrategia
didáctica para la enseñanza/aprendizaje de la programación: Tecnológicas,
ISSN-p 0123- 7799 / ISSN-e 2256-5337, Vol. 21, No. 41, enero-abril de 2018, pp.
115-134. http://www.scielo.org.co/pdf/teclo/v21n41/v21n41a08.pdf
18.
Romero, G. (2009). “La
utilización de estrategias didácticas en clase”. Innovación
y Experiencias Educativas, pp. 3-5. http://vip.ucaldas.edu.co/latinoamericana/downloads/Latinoamericana11(1)_Completa.pdf
19.
Salas,
L. (2000). La investigación-acción, su importancia y aplicación en la
educación. Revista
Scientae & Methodus, 67-84.
https://revistas.uancv.edu.pe/index.php/SM/article/view/728
20.
Sandoval, C. (2020). La educación
en tiempo del covid-19 Herramientas TIC. Revista Tecnológica-Educativa
Docente,
24-31. https://ojs.docentes20.com/index.php/revista-docentes20/article/view/138
21.
Santacruz, H. (2010) La
etnia Pasto y su cultura. Composición fotográfica Mono Lasso.https://historiadelartecolombiano.files.wordpress.com/2015/04/pasto-y-su-cultura.pdf
22.
Vargas,
G. & Gamboa, A. (2013). El Modelo de Van Hiele y la enseñanza de la Geometría.
Uniciencia,
Vol.
27, No. 1 pp. 74-94. https://www.redalyc.org/pdf/4759/475947762005.pdf
23.
Vásquez,
F. (2005) Pregúntele
al ensayista. Bogotá:
s.n., pp. 159-202. http://www.iesseneca.net/iesseneca/IMG/pdf/Conectores_textuales.pdf