http://dx.doi.org/10.22267/rtend.151601.32

CRITERIO DE LAPLACE: PREMISA FUNDAMENTAL EN INDUCCIÓN ESTADÍSTICA

LAPLACE CRITERION: FUNDAMENTAL PREMISE IN STATISTICAL INDUCTION

Por: Emilio José Chaves¹

¹ Ingeniero Mecánico, Universidad de los Andes. Investigador independiente. Correos electrónicos: chavesej@hotmail.com, ejotach@gmail.com

Resumen

Palabras clave: Inducción estadística - Modelos de ajuste – Métodos numéricos – Curvas de Lorenz y FDA – Muestras aleatorias

Clasificación JEL: C14

Abstract

It discusses the rule or Laplace Criterion and fundaments its use to build the Lorenz Curve, LC, from datasets. It presents samples and graphs of inferred fitting models of LC and CDF; it comments the limits of the model. Method separates real media U, from adimentional CDF to work it as CDF(real)=U(real)*CDF(in medias). The purpose is to give fundamentals to univariate statistical inference of positive datases using Laplace Criterion, standard mathematics and Boolean sets theory. This nonparametric method assumes identical 1/N frequencies for N data without using a priori distribution functions. Given its simplicity, it is proposed to apply it in statistical education and research as a theoretical element, prior to the handling of multivariate analysis.

Key words: Statistical induction fundamentals – Fitting models – Numerical methods – Lorenz Curves and CDF – Random samples.

Classification JEL: C14

Introducción

El control de calidad de los modelos matemáticos de inducción, inferencia, o regresión estadística hechos a partir de series de datos, es un tema esencial de tipo epistemológico y práctico en la investigación científica y en la sociedad actual. Las fallas de calidad son originadas en parte por la dificultad empírica para saber a tiempo si una muestra hecha con datos parciales es suficientemente representativa, en parte por las deformaciones incorporadas por el azar de ellas, y en parte por los procedimientos y métodos usados para modelar y graficar las curvas de interés. En este análisis el error de medición se considera un problema menor que debe ser detectado y tratado por separado.

Las series de datos de dimensión N grande suelen conducir a mejores resultados inferenciales, pero dos muestras de igual dimensión N pueden poseer calidades distintas al respecto; a las mejores las llamamos “más representativas”, aunque es difícil definir si una muestra lo es, justificar por qué lo es, y aún más, hacerlo a tiempo. Para ello necesitaríamos conocimiento perfecto y anticipado del fenómeno, y esa es precisamente la meta deseada o finalidad del proyecto inferencial. Toda inferencia busca proponer una buena imagen del fenómeno en su conjunto (modelo) para obtener conclusiones generales y tomar decisiones apoyadas en el modelo resultante. Esto es hecho a partir una serie de datos del fenómeno que son tomados y medidos dentro de un contexto concreto y específico de investigación con datos siempre parciales.

Luego de una medición de N casos, solo conocemos la serie de N datos medidos, pero ignoramos totalmente sus frecuencias reales. Laplace señaló que en las inferencias es necesario aportar premisas o supuestos a priori que llenen ese vacío y faciliten la tarea; estos deben declararse al inicio de todo reporte y requieren justificación. Una premisa muy empleada y quizás poco reflexionada es el llamado Criterio de Laplace, consistente en asumir que cada uno de los N datos medidos en una serie de datos, Ki, posee la misma frecuencia 1/N de casos de la población receptora que se defina.

Esta premisa permite estimar el valor aproximado de la media U como el promedio aritmético de los datos. Al aumentar la dimensión N de la muestra, la U estimada suele acercarse a la media real y mejorar la calidad de los resultados, pero N no puede ser muy grande por razones prácticas. Cuando toma mucho tiempo recoger una muestra N grande, la realidad final ya no refleja el instante sino un lapso mayor de tiempo con sus cambios dentro de este.

El texto estudia y aplica esa premisa para construir modelos continuos de la Curva de Lorenz, CL, y la Función de Distribución Acumulativa, FDA; desarrolla dos modelos distintos de ajuste a ellas y los aplica, primero a una serie de datos teórica usada como referente y luego a otras series aleatorias con N=10 datos, consideradas como ejemplos de N pequeño. El objetivo es mostrar resultados y sus gráficos, observar su precisión y las diferentes distorsiones que pueden darse entre los datos y los resultados del modelo trabajado. En resumen, es una simulación aplicada a datos generados por un modelo inicial prediseñado que se asume como fenómeno perfecto.

Intencionalmente, se emplea un modelo referencial que no es lineal, ni simétrico; es ajeno a cualquier distribución paramétrica. La idea es inferir el modelo resultante a partir de los datos y pocas premisas, usando a fondo las propiedades del Criterio de Laplace y de la Curva de Lorenz.

Los resultados señalan que las distorsiones tienen varias causas como la aleatoriedad, los límites matemáticos implícitos en cualquier modelo y sus premisas implícitas. Tener conciencia temprana de esas premisas y límites ayuda a entender la lógica del método y a defender la importancia de la coherencia y transparencia en la argumentación –verbal y/o matemática–. Esto debe exigirse en estadística inferencial, sea en el caso más sencillo univariable que nos ocupa, o en otros multivariables más complejos que vendrían después de aclarar el caso univariable.

He trabajado de manera independiente esta línea de investigación inferencial durante las últimas dos décadas; sin embargo, solo recientemente abordé el estudio cuidadoso de la premisa de Laplace cuando entendí que la usaba sin advertirlo. En este caso personal, primero se dio la experiencia práctica y más tarde la fundamentación teórica del método, de sus posibilidades y de sus límitaciones. El motivo inicial para emprender tal camino fue el deseo de superar mi dificultad para comprender los cursos y textos universitarios de estadística hace más de cuarenta años. En el proceso debo agradecer la lectura de varios artículos críticos de otros analistas inconformes con la marcha de la disciplina, cuyo número ha crecido durante los últimos años.

La lección más importante para esto la recibí del profesor alemán de filosofía Ernest Bein en mis últimos años de colegio, cuando nos enseñó en el aula que todo texto de filosofía emplea premisas que el lector debe buscar hasta hallarlas y reflexionar sobre ellas. Decía que los más honestos las declaran abiertamente al comienzo, otros las presentan en algún pie de página o en algún párrafo intermedio; solo hay que detectarlas y emplearlas para identificar los méritos y las incoherencias que pueda presentar la obra y ante todo, para interpretarla, reaccionar ante ella y darle sentido propio a la cuestión.

Los gráficos y tablas del artículo se presentan en inglés. Se espera que no obstaculice mucho la comprensión para los lectores en idioma español.

El criterio de Laplace vinculado a las curvas de Lorenz

Un artículo estadístico (Campos, 2014: 64) estudia pasajes del libro de Laplace “Ensayo filosófico sobre las probabilidades” y cita un párrafo donde Laplace resume lo que hoy es conocido como el Criterio, o Regla de Laplace:

La teoría del azar consiste en reducir todos los acontecimientos del mismo tipo a un cierto número de casos igualmente posibles, es decir, tales que estemos igual de indecisos respecto a su existencia, y en determinar el número de casos favorables al acontecimiento cuya probabilidad se busca. La proporción entre este número y el de todos los casos posibles es la medida de esta probabilidad, que no es, pues, más que una fracción cuyo numerador es el número de casos favorables y cuyo denominador el de todos los posibles.

Tal como lo interpreto, Laplace crea aquí la premisa al afirmar que la teoría del azar lleva a actuar en un contexto de indecisión que se modera si tales acontecimientos se reducen a la calidad de “equiprobables”, y que el denominador de la probabilidad que “se busca” es “el de todos los casos posibles”. O sea, asigna a priori la frecuencia 1/N a cada uno de “cierto número” N limitado de acontecimientos observados; y reconoce que busca la probabilidad porque no dispone de ella. En la frase está implícito que busca y entrega una propuesta de premisa para llenar la ignorancia inicial sobre las frecuencias, porque los datos no traen consigo una etiqueta que diga “mi frecuencia real es 1/20 y es distinta a la de los demás datos de la serie”.

Ese mismo problema lo abordan los análisis paramétricos asumiendo un modelo a priori, como es el caso de la distribución Normal, o campana de Gauss, sin mencionar que, al sacar el promedio U como paso inicial, también están adoptando una segunda premisa: la de Laplace. Esta premisa es muy sensata dada la situación y ha contribuido al desarrollo del análisis inferencial de datos. Toda premisa contiene un elemento necesariamente subjetivo y crea el compromiso de sostenerla en la interpretación que se haga con ella.

Ahora entramos en otros aspectos del tema. Por simplicidad en el manejo, aquí es asumido 1) que los datos de la serie se ordenan en descenso antes del análisis, o sea, de mayor a menor; y 2) como no hay errores de medición, los datos que conforman la muestra, son al menos representativos de sí mismos, tal cual son presentados para el análisis. Esto significa que el análisis estadístico no cuestiona los datos recibidos, solo los interpreta. Una vez emprendido el camino, nos hacemos rehenes de los datos, de las premisas iniciales, y del modelo propuesto en el proceso –que también aporta premisas. Toda incoherencia que se presente debe ser atendida y resuelta; de no hacerlo, el modelo pierde calidad, seriedad y vigencia.

La premisa de Laplace trae otras consecuencias poco estudiadas; el objeto de este artículo es desarrollarlas y sacar provecho de ellas. Las más notables –que no menciona Laplace– son:

1) Si calculamos la media U como el promedio de los N valores medidos, Ki, entonces también está implícito el supuesto de que cada Ki se comporta como el promedio de un sector pequeño, entre límites desconocidos K_i-1 y _Ki+1, con frecuencia 1/N. Estos límites deben ser estimados en algún momento, con ayuda del modelo matemático que surja en el análisis y no deben superponerse con los sectores vecinos (overlapping en inglés) porque se trata de sectores disyuntos, ordenados en descenso y continuos. Su agregación produce el conjunto total.

2) La media estimada U implica que la masa repartida M puede estimarse como M = U*N …. [1]

3) La contribución a la Curva de Lorenz en fracción de cada Ki y su intervalo respecto a la masa es

4) Si algún sector posee Ki=0 significa que su media es nula y que su fracción 1/N no recibe nada en la distribución, está excluido de ella. Esto afecta la media U, la forma de la distribución y las gráficas resultantes.

Si efectuamos Ki/U para cada dato, obtenemos el valor de la variable en medias de la distribución de cada sector i, entonces la unidad de medición se hace adimensional, @. Esto permite dejar temporalmente de lado el valor y las unidades de la media real U# y concentrarnos en la distribución K adimensional. Una vez hecho esto, reintegramos al final U#, de modo que K# = U# * K(x)@.

Esto hace posible determinar N puntos de la curva de Lorenz como:

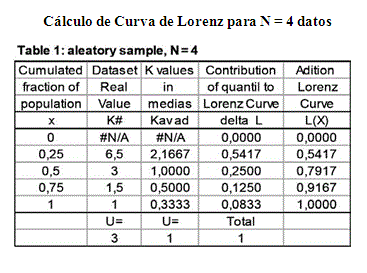
(X, L) = (i/N; S1i Ki/NU …. [3] … X es la fracción acumulada de población –que suele ir en el eje horizontal X y L es la participación –de la población acumulada X de más cuantía– en la masa total distribuida, para el ordenamiento descendente de la variable, aquí empleado. El Anexo 1 muestra un ejemplo numérico que parte de 4 datos y realiza el procedimiento explicado hasta ahora.

5) Cuando el mismo valor se repite en la muestra, la frecuencia aumenta para el mismo valor.

Una curva de Lorenz para datos ordenados en descenso siempre va del punto (0;0) al punto (1;1), viaja por encima de la diagonal, es creciente y si sobrepasa el valor Y=1, significa que la masa total repartida ya está agotada y hay un sector de población excluído del reparto que debe aparecer en las gráficas resultantes –esto se arregla dando el valor 1 a L cuando sobrepasa L=1- . Si baja de la diagonal, o sea Y<X significa que los datos no quedaron bien ordenados en descenso.

Si contamos con cuatro puntos de la CL, por ejemplo, los correspondientes a los cuantiles 0 a 0,25 – 0.25 a 0,5 – 0.5 a 0,75 – 0.75 a 1.0, además del puntos (0,0) del extremo izquierdo, es posible inferir una curva suave aproximada de grado 4, usarla como modelo que pase por dichos puntos y graficarla.

Hecho esto, basta con derivar el modelo obtenido de la curva de Lorenz y se obtiene la FDA@, en medias de la distribución, la cual es una curva estructural y adimensional, como lo es la CL. Desde esta perspectiva la CL y la FDA son las dos curvas continuas más importantes en inferencia estadística aplicada a casos univariables positivos. Podemos dejar de lado la Función de Densidad de Probabilidad, FDP, muy empleada en estadística tradicional durante los últimos dos siglos; es secundaria. Si se desea, es posible calcularla a partir de la FDA obtenida antes.

El siguiente aparte presenta un ejemplo numérico concreto que explica el método y discute algunos límites de los modelos que afectan los resultados y su interpretación final.

Ejemplo numérico referencial: Serie de datos con N=10

Como ejemplo, sea una función descendente particular de la FDA: (K >= 4-3x², cuyo promedio estimado con integrales es U=3, para población entre 0 y 1).

Se calcula la fracción total del área que corresponde a cada decil, primero de x=0a0.1 luego de 0.1a0.2 y así hasta 0.9 a 1. Luego tomamos el valor Ki promedio de cada decil y lo dividimos por U=3 y así resultan 10 datos promedios Ki @ adimensionales, que conforman la serie de datos a trabajar. Por otro lado, agrupando esos datos, obtenemos 10 puntos de la curva de Lorenz correspondientes a los N sectores de igual frecuencia 1/N. Esos 10 puntos que conforman la serie de datos referencial de las medias del ejemplo son:

Serie: (3.99; 3.93; 3.81; 3.63; 3.39; 3.09; 3; 2.31; 1.83; 1.29)

Y su promedio esperado es U=3, resultante de aplicar la premisa de Laplace.

El siguiente paso es graficar esos valores para los puntos intermedios de cada decil obtenemos 10 puntos (0.05, 3.99), (0.15, 3.93)…. (0.85; 1.83) y (0.95; 1.29). Se anota que estos puntos son aproximados, ya que los valores de la serie de datos van algo corridos a la izquierda del punto medio de su intervalo y se trata de una curva en descenso. Si fuera una línea recta descendente, irían en el punto medio de cada decil. La Gráfica 1 muestra esta curva referente de datos aproximados, hecha con las medias exactas de cada decil a partir de la fórmula escogida K=4-3X².

2) Las Gráficas 2 y 3 muestran 10 puntos exactos de la FDA o K (X) conformada por el modelo. Al aplicar la función Tendencia de Excel (MR), esta arroja la siguiente ecuación formulada por el computador en base al método de Mínimos Cuadrados:

K(OLS) = -10^-13x3 - 3x² + 10^-13x + 4… eliminando insignificancias da: K>=(en unidades reales)= 4 - 3x² … [4] …. Igual al modelo referencial.

3) La Gráfica 2 muestra la anterior función K exacta junto a los valores de la serie de datos, hecha de medias exactas de cada sector 1/N, situados en la mitad de los intervalos. Al aplicar el método OLS de Excel, o sea el de mínimos cuadrados, se obtuvo la ecuación:

K#(OLS) = 10^–13x3 - 3x² + 10^–12x + 3,9975 …[5] Eliminando insignificancias: K#(OLS) = 3,9975 - 3x² … [6] … similar a [4]

4) Al construir la CL aplicando el criterio de Laplace se obtiene la Gráfica 3, cuya ecuación obtenida con el método OLS resultó: L(OLS) = -4*10^–12x⁴ – 0,3333x³

L(OLS) = – 0,3333x3 + 1,3333x … [7]

2a) La integral de [4] debe producir la curva de Lorenz, o sea

L(x) = – (1/3)x³ +1,3333x … [5] sin constante porque L(0)=0

3) También la Gráfica 1 muestra el modelo de Mínimos Cuadrados para la función Curva de Lorenz, (L = – 5*(10–¹²) x⁴ – 0,3333 x³ – 6 *(10–¹²) x² + 1,3333 x – 2*(10^–12)), la que una vez simplificada de componentes insignificantes se convierte en:

L = - 0,3333x³ + 1,3333x … [6] …. Cuya derivada en medias es: Kadimensional = 1.3333 – X² …. Y multiplicada por U = 3 produce: Kadimensional= 4 – 3X² … idéntica a la función K referencial.

4) Este resultado casi exacto del método OLS se debe a que fueron empleadas ciertas condiciones poco frecuentes en la realidad, tales como:

a) La función inicial es muy sencilla y se diseñó en base a exponentes enteros como los que emplea el OLS (mínimos cuadrados). Los modelos de la realidad pueden ser más complejos y pueden contener exponentes fraccionarios –no enteros–.

b) Se emplearon medias exactas de cada sector 1/N para conformar la serie de datos, o dataset, lo cual genera una media U exacta. La probabilidad de que esto ocurra en muestras aleatorias existe pero es mínima, lo más probable es que la media U resulte algo distinta de la real.

Lo importante de este experimento controlado es que muestra la coherencia entre la teoría matemática, la lógica Booleana de conjuntos y los fundamentos teóricos del método y sus premisas cuando se aplica estrictamente el Criterio de Laplace.

5) Los 10 valores reales K# de la serie trabajada conducen al valor exacto de la media real U=3. Si los usamos para crear 5 valores de frecuencia 1/5, promediando cada par consecutivo, el resultado obtenido de U y de las gráficas también resulta casi perfecto.

6) En este ejemplo teórico no es necesario emplear una muestra de N grande.

El siguiente paso es investigar qué ocurre cuando la muestra es aleatoria y porta cierta representatividad mediante un diseño hecho para ello.

Al comenzar un análisis inferencial no conocemos las frecuencias de cada valor medido Ki, ni la media real, ni los dos valores de K dentro de los cuales está insertado Ki. Aquí es donde aplicamos el Criterio de Laplace como premisa sencilla que postula igual frecuencia 1/N para los Ki disponibles, ya que no disponemos de

opciones mejores. Generalmente, aunque no siempre, aumentar las mediciones N mejora los resultados. Esto se debe a los avatares del azar. Pero si asumiéramos sin

Generación artificial de N=10 datos aleatorios de la muestra

Ahora vamos a generar muestras algo representativas con valores aleatorios–distintos a los promedios verdaderos y veremos que las funciones inferidas presentan cierto isomorfismo algo distorsionado respecto a las gráficas de referencia, que la media U resulta algo diferente, que también los tests R2 (Chi-cuadrado) bajan algo su calidad, y rebaja la calidad de la inferencia para valores N pequeños. Sin embargo, los resultados muestran ajustes de calidad e isomorfismo aceptable en las gráficas obtenidas. Los 10 valores aleatorios obtenidos se presentan a continuación; su media U=3.0641, es algo superior a la Ureal=3 de referencia.

(3.9752 3.9112 3.8065 3.6471 3.3203 3.2197 2.6773 2.6372 1.8983 1.5484)

Una vez construida la tabla de Lorenz siguiendo las instrucciones dadas, y graficados sus valores para cada decil se obtuvieron las Gráficas 4 y 5.

Ambas curvas de Lorenz, la real y la aleatoria son visualmente parecidas. Usando el método de mínimos cuadrados, OLS, las ecuaciones obtenidas de grado 4 resultan algo diferentes; pero si los valores de K de ellas se multiplican por la media respectiva de U=3real y de U=3.0641 entonces puede verse en la Gráfica 5 que los dos modelos son aproximados entre x=0 y x=0.65, y difieren en la cola baja a la derecha. Esta deformación para una muestra particular, fue causada por la aleatoriedad que alteró la media y la forma. Si usamos otra muestra de N=10 la deformación y el valor U distinto producen otras alteraciones distintas, pero en general, se observa que el ajuste entre el modelo y la realidad es aceptable pero imperfecto, aunque la muestra no sea muy representativa.

Si aumentamos la muestra a N=20 los resultados mejoran En general una muestra de N=40 es buena y una de N=100 sería excelente y más que suficiente en la mayoría de las investigaciones. En este sentido el método aquí discutido difiere de la estadística convencional que recomienda realizar miles de datos para arreglar sus dificultades analíticas cuando descubren incoherencias en sus gráficas y tests de calidad.

Hay infinidad de muestras posibles de dimensión N=10 datos y no hace falta analizar más casos como el exhibido. El ejemplo basta para mostrar que hay cierto isomorfismo cuando se trabaja el método OLS con nivel 4 y ecuación tipo (a+bx+cx²+dx³+ex⁴). El método OLS funciona mejor cuando se seleccionan unos 5 datos para exponente de nivel 4. Si se emplean exponentes altos se presentan con frecuencia ondulaciones entre cada par de puntos, aunque el ajuste a los puntos conocidos sea muy bueno y el test R2 (chi-cuadrado) dé valor 1. Esto se debe a que los modelos matemáticos también poseen límites que contribuyen a deformar el resultado y es preciso controlarlos para que no se presenten incoherencias inaceptables. Afortunadamente, un analista puede simplificar el modelo matemático para moderar esas distorsiones sin alterar las series de datos originales.

La media resultó U=3.064 para la Serie 2. Este valor es algo más alto que U=3 de la Serie 1 de referencia. Esto hace que los puntos estimados de L bajen un poco en comparación con la curva de Lorenz real: se aplasta L en algunos sectores, se eleva en otros. Pero al reintegrar K@ con U# para obtener la función K# = U# * K@ (en medias), esta se hace similar a la función referencial K# de diseño, aunque presenta algunas distorsiones en la cola baja atribuible al azar de la muestra de ejemplo que produjo un bajo valor de U. Si bien las dos curvas de Lorenz, la referencial y la inferida son visualmente muy parecidas, las pequeñas diferencias entre ellas causan que sus derivadas K@ presenten diferencias mayores, las que parecen autocorregirse algo al final del proceso. Esto se debe a que la función K es la derivada de L; es necesariamente muy sensible a los valores teóricos de la Curva Lorenz: al cambiar U, cambia ligeramente la curva Lorenz y cambia el modelo que lo representa, y su derivada K lo hace mucho más; y al reintegrar K#=U*K@ la distorsión baja, pero aparecen algunas diferencias como las observadas en el gráfico.

Prediseño y simulación de ejemplos

El procedimiento empleado parte de definir K(x) para llegar a la CL. Hay otros métodos; por ejemplo si la curva Lorenz tiene forma L=ax+bx²+cx³+dx⁴, es posible asignar valores a los coeficientes(a,b,c,d) y mediante ensayos de prueba y error llegar a una forma válida. Este método es laborioso y largo, aún con la ayuda de computadores portátiles.

Otro método es este: si suponemos una función W(x) por ejemplo, W=0.6-0.6x^1.5 y que L(x)= x^W(x), al graficarla puede cumplir los requisitos de una CL para datos en descenso. La derivada de esta CL es

Debe tenerse en cuenta que los valores empíricos de W(Xi) se pueden estimar a partir de los puntos conocidos de (xi acumulada; Li) como Wi = ln(Li)/ln(xi acumulada).

Al aplicar este modelo también deben tomarse precauciones para evitar que

K>=(x) presente ondulaciones que rompan la premisa del orden descendente. Este modelo es particularmente eficaz para ganar experiencia sobre la infinidad de distribuciones que son posibles, para generar muestras aleatorias de cualquier tamaño N sin apelar a bases de datos externas, y para el análisis estadístico de series de datos generadas a partir de cualquier curva paramétrica.

Conclusiones y comentarios

• El Criterio de Laplace es una premisa simple que permite fundamentar la inferencia estadística cuando se vincula a la Curva de Lorenz.

• Debido a los avatares del azar en las muestras y a los límites y efectos del método y del modelo escogidos, las inferencias de este tipo son siempre aproximaciones útiles si se tiene en cuenta el estado de ignorancia inicial cuando solo disponemos de la serie de datos.

• Nunca sabemos si la media U estimada de la muestra está por encima o debajo de la media real desconocida. Esa diferencia influye sobre la curva de Lorenz. Cuando U es mayor, en algunos sectores se deforma algo la CL construída con el Criterio de Laplace. Cuando U es menor, ocurre lo mismo. Igual pasa con la FDA o derivada de L. La deformación se autocorrige algo al reintegrar el promedio U# a las funciones adimensionales L y K.

• El método mostrado se basa solo en la serie de datos. No necesita emplear distribuciones estructurales a priori, que luego presentan como posteriores tal como hacen los métodos paramétricos.

• Cuando aplicamos K# = U# * K@ se conserva la integridad de las unidades trabajadas, de modo que si cambiamos –por ejemplo U=2 metros/media a U=2000 milímetros/media, se conserva la coherencia dimensional del análisis. Muchos fenómenos pueden describirse entonces como el efecto combinado de la dimensión U y la función estructura distributiva adimensional K@.

• Es importante reconocer la experiencia y los criterios de los investigadores en cada campo de su labor. Antes de que apareciera la estadística ellos hicieron magníficas contribuciones a la ciencia y la técnica usando herramientas sencillas, modelos intuitivos y criterios propios. Este trabajo busca facilitar una herramienta estadística sencilla y fundamentada para apoyar a los investigadores. Basta aplicarla con un computador personal, un programa Excel o su equivalente, y criterios sencillos para hacer análisis estadísticos preliminares. Estos suelen darse cuando aparecen los primeros resultados de medición y se necesita evaluar el rumbo general que toma la primera muestra hecha de pocos datos.

• Aunque el tema de las distribuciones secuenciales no es tratado, el método ha sido empleado en este campo con buenos resultados. Esto podría ser útil para los investigadores de bioestadística, aseguradoras de riesgos y control de calidad de productos.

• En muchos análisis preliminares basta una muestra de N=10 para obtener un resultado que posee isomorfismo aproximado con la distribución real. Con N=20 mejora mucho el resultado. N=100 es muy buena; usar más de 100 datos es innecesario en la mayoría de estos casos univariables. Definir un N adecuado depende también de las características del objeto investigado. Por ejemplo, en bioestadística es difícil disponer de muestras grandes en ciertos casos, y es posible usar N entre 4 y 10 advirtiendo que los riesgos de distorsión se hacen mayores.

REFERENCIAS

1. CAMPOS, Alberto (2004). Laplace: Ensayo filosófico sobre las probabilidades. Revista Colombiana de Estadística. Vol. 27, No. 2, p. 64.

2. LAPLACE, Pierre Simon de (1902). A Philosophical Essay on probabilities. John Wiley and Sons. Translated from 6th. (French edition). Ps 11-12 and 61. Consulted in Sept/04/1914 at https://archive.org/ stream/philosophicaless00lapluoft#page/n5/mode/2up.

Tabla de ejemplo de Apéndice 1