http://dx.doi.org/10.22267/rtend.161701.11
BREVES CONSIDERACIONES ACERCA DE LA IMPORTANCIA DE LOS ÁRBOLES DE DECISIÓN EN EL ANÁLISIS DE CARTERAS
BRIEF CONSIDERATIONS ABOUT THE IMPORTANCE OF DECISION TREES IN PORTFOLIO ANALISYS
BREVES CONSIDERAÇÕES SOBRE A IMPORTÂNCIA DOS
ÁRVORES DE DECISÃO EM O ANÁLISE DE PORTFÓLIO
Por: Julio César Riascos -Jesús Enrique Molina
Magister en Gerencia y Asesoría Financiera, Universidad Mariana, Profesor e investigador Universidad Mariana y Universidad de Nariño. Integrante de los Grupos de Investigación CONTAR, Coyuntura Económica y Social y FRONTERA SUR. Email: jriascos2009@hotmail.com
Magister en Finanzas, Universidad EAFIT, Profesor e Investigador Universidad Mariana. Integrante del Grupo de Investigación CONTAR. Email: jemolinam2003@yahoo.com.ar
Recibido: 09 de agosto de 2015 Aprobación definitiva: 10 de octubre de 2015
Resumen
La cada vez más estrecha relación entre las ciencias y/o disciplinas no es ajena a la relación derivada en los últimos 50 años entre las finanzas, la Econometría, la modelación estadística y los procesos de simulación computacional. El propósito de este artículo introductorio reside en exponer algunas breves consideraciones con respecto al potencial manejo de los árboles de decisión en la teoría financiera y particularmente como complemento al diseño de los tradicionales árboles de rentabilidad. El documento sugiere que la importancia atribuida a los árboles de rentabilidad así como el modelamiento de carteras propios de la teoría financiera debe ser complementada y afianzada por herramientas de simulación cuya aplicación posibilita anticipar situaciones futuras y elaborar políticas ex-ante. De acuerdo con lo anterior, se refuerzan los análisis de un portafolio de inversión a través de árboles de decisión bajo tres escenarios que comprenden diferentes combinaciones de riesgo y rentabilidad. Mediante este ejercicio no complejo, se concluye que las rentabilidades de una cartera de inversión asociadas a los escenarios planteados arrojan resultados diversos que dependen de la probabilidad estadística de ganar o de perder.
Palabras clave: Árboles de decisión financiera, Árboles de rentabilidad, Decisiones de Inversión, Carteras de Inversión.
JEL: G11.
Abstract
The special relationship between finance, econometrics, statistical modeling and computational simulation processes has experimented an increase in the last 50 years. The aim of this paper is to explain some considerations related to the potential application of the decision trees in financial theory and particularly as a complement in the design of traditional profitability trees. This paper suggests that the relevance attributed to profitability trees as well as portfolio modelling in financial theory, must be supplemented and secured by simulation tools which allows to anticipate future scenarios and the development of exante policies. Therefore, the analysis of an investment portfolio is reinforced through profitability trees, particularly, aslant three different combinations of risk and profitability. This exercise allows to conclude that the returns of an investment portfolio related to the proposed scenarios show different results based on the Statistical probability of winning or losing.
Keywords: Financial decision trees, profitability analysis trees, Investment decisions, Investment Portfolios.
JEL: G11.
Resumo
O cada vez mais estreita relação entre ciência e/ou disciplinas não é estranho para a relação derivada nos últimos 50 anos entre as finanças, a Econometria, modelagem estatística e processos de simulação computacional. O objetivo deste artigo introdutório encontrase em expor algumas breves observações a respeito do potencial de árvores de decisão, em na teoria financeira e particularmente, para complementar o projeto de árvores tradicionais de rentabilidade. O documento sugere que a ênfase em árvores de rentabilidade e carteiras de modelagem próprios da teoria financeira deve ser complementada e reforçada pelas ferramentas de simulação como aplicativo para antecipar possíveis situações futuras e desenvolver políticas ex-ante. De acordo com o exposto, a análise de uma carteira de investimento por meio de árvores de decisão em três cenários compreendendo diferentes combinações de risco e retorno são reforçadas. Através deste exercício não é complexo, concluise que os retornos de uma carteira de investimento relacionado com os cenários propostos produzir resultados diferentes que dependem da probabilidade estatística de ganhar ou perder.
Palavras-chave: Árvores de decisão financeira, Árvores de rentabilidade, Decisões de Investimento, Carteiras de Investimento.
JEL: G11.
Introducción
Una de las principales preocupaciones de la moderna teoría financiera reside en el desarrollo de instrumentos, políticas, operaciones e instituciones que posibiliten el sustento necesario para optimizar la toma de decisiones de inversión. Según Adam Smith, la resolución de un individuo al arriesgar su capital en una actividad productiva estaba alimentada por la promesa de un rendimiento. No obstante, el propio padre de la economía sentenció que “aun cuando los beneficios ordinarios del capital suelen aumentar con el riesgo, no siempre suelen hacerlo en la misma proporción” (Smith, 1997: 108-109). Esta importante observación sugiere la existencia del concepto de incertidumbre, lo que implica, que las expectativas que impulsan al inversionista a emprender una actividad que comprometa sus recursos, están sujetas a una infinita cantidad de contingencias que pueden afectar de forma significativa los resultados de una inversión en un momento determinado.
Al definir el concepto de inversión Alexander, Sharpe y Bailey sostienen que éste se relaciona con el sacrificio de una proporción de recursos efectuado por el inversionista en un tiempo presente con el propósito de obtener un volumen superior de dinero en un periodo futuro que, advierten se caracteriza, en todo caso por ser incierto (Alexander, Sharpe y Bailey. 2003). Precisamente es esa incertidumbre la que implicó ingentes esfuerzos por pronosticar el futuro desde el siglo XVII, proceso que floreció bajo el auspicio de herramientas de análisis estadístico y que a la postre justificó el reciente y acelerado desarrollo de la econometría financiera. (Engle, 2001); (Bollerslev, 2001) y (Tauchen, 2001).
Los registros históricos de las empresas y de los individuos permiten evidenciar explicaciones, comportamientos, factores determinantes y efectos de un conjunto de variables como por ejemplo, las tasas de interés, el crecimiento de las ventas, la evolución de los pasivos no corrientes, la inflación, las utilidades, entre otros. No obstante, esta información, que generalmente es aceptable para la comprensión de los fenómenos históricos, resulta por demás insuficiente para advertir los cambios que se generarán en el futuro y que comprometen las decisiones de inversión concebidas por los agentes participantes en tiempo presente, así como el comportamiento de los sectores, la estabilidad macroeconómica, el equilibrio internacional y finalmente el logro de objetivos sociales.
A fin de dar respuesta a la gran interrogante que implica la existencia de la incertidumbre en las decisiones financieras, la metodología de trabajo ha hecho un uso extensivo de modelos. La mayor parte de los procesos de modelación financiera esgrime rudimentos de estadística y econometría de series de tiempo, esencialmente aplicadas al seguimiento de los precios de un activo financiero como una acción, un bono, una divisa, incluso para el pronóstico de los mercados a través de una serie de supuestos que permiten la recreación de diversos escenarios y el diseño preventivo de políticas económicas o financieras que minimicen la presencia de factores perturbadores y maximicen la probabilidad de materializar los objetivos deseados hacía el futuro (Hanke y Wichern, 2010: 553).
Las aparentes dificultades de este tipo de herramientas de análisis señalan que la complejidad intrínseca en el diseño de modelos matemáticos ARIMA y sus correspondientes familias o los modelos ARCH (Gujarati y Porter, 2010: 921) y sus derivaciones, no necesariamente implican predicciones aproximadas donde se señalen los elementos determinantes sobre los cuales desarrollar la política económica o financiera por cuanto son modelos a-teóricos (Bermejo, Torres y Masferrer, 2009). No obstante, un investigador puede implementar un diseño de modelo ARIMA o ARCH e incorporar sin mayor dificultad ejercicios computacionales que involucren variables teóricas sobre las cuales implementar algún tipo de política. Frente a la capacidad predictiva, pese a los esfuerzos que en esta materia se han desarrollado, independientemente del arquetipo de diseño, los pronósticos se han caracterizado por imprecisiones que, en todo caso se refieren a que los out-put entregados por un proceso de modelaje deben resolverse como la aproximación a una tendencia futura más que al encuentro indefectible de una situación definitiva.
Con respecto a la relevancia de los factores determinísticos y, los factores estocásticos que imprimen incertidumbre, Olaya Pardo (2002) plantea que “la formulación teórica podía ser resultado de la combinación de análisis sobre los hechos y razonamientos deductivos sobre el comportamiento de las variables. De esta manera, demostraron que si era posible tener una teoría con múltiples soluciones para los diversos casos. Las decisiones en finanzas dependen del análisis de variables reales, por tanto, la teoría surge cuando se reconoce la importancia de la incertidumbre y se hace necesario establecer principios que permitan predecir el comportamiento futuro de las variables sobre las cuales se toman decisiones” (Olaya Pardo, 2002: 6).
LA IMPORTANCIA DE LOS PROCESOS DE SIMULACIÓN
De otra parte, la teoría matemática posibilita una importante herramienta de estudio en el campo de la simulación que “consiste básicamente en construir modelos informáticos que describen la parte esencial del comportamiento de un sistema de interés, así como en diseñar y realizar experimentos con el modelo y extraer conclusiones de sus resultados para apoyar la toma de decisiones” (Ríos Et. Al, 2009: XII). Las simulaciones constituyen representaciones matemáticas de modelos que permiten crear escenarios de respuesta ante decisiones tomadas por un inversionista, de tal modo que permiten anticipar las consecuencias de una determinada disposición.
Las decisiones de inversión son dinámicas, esto implica que, las determinaciones que los agentes económicos tomen en un punto del tiempo, tienen un efecto sobre las decisiones que llevarán a cabo en un momento subsecuente o posterior. (Vitoriano, Begoña, 2007: 10). En este tipo de situaciones, tanto la formación de expectativas como las acciones proferidas por los individuos tienen en consideración sus implicaciones futuras de manera secuencial y esto mismo, conlleva a que las soluciones abarquen procesos de atrás hacia adelante (Tarzijan y Paredes, 2012: 192), es decir que examinen las causas y las subsecuentes consecuencias inherentes a cada decisión.
Una situación implica el análisis de los agentes económicos involucrados y, a su vez promueve una serie de posibilidades con las cuales se pretende enfrentar un determinado fenómeno. El desarrollo de dichas posibilidades supone la existencia de escenarios que, en parte, dependerán de los diferentes abanicos de opciones estudiadas por los participantes y por supuesto, conllevan una serie de expectativas secuenciales y condicionadas a su probabilidad de ocurrencia. Para ilustrar el tema de las decisiones piénsese por ejemplo en el objetivo financiero básico que reside en maximizar el valor de la empresa en el mercado. La generación de valor constituye uno de los temas de mayor preocupación en la literatura financiera moderna y el consenso sobre sus factores determinantes advierte que el capital intelectual confiere un 75% de contribución a la generación de valor o riqueza para una empresa mientras que, el 25% restante se relaciona con el manejo del capital financiero (Ordóñez de Pablos, 1999).
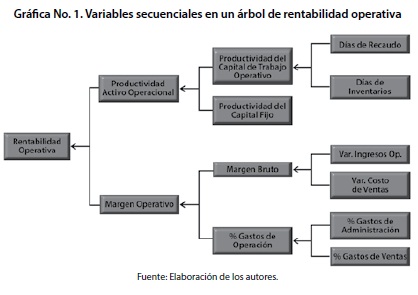
Dentro de una óptica financiera, la generación de valor depende de la rentabilidad operativa de los activos netos y del costo promedio ponderado de capital. A su vez la rentabilidad operativa de los activos netos depende de la productividad de los activos operacionales y su margen operativo. La productividad del activo operacional se explica por la productividad del capital de trabajo y la productividad del capital fijo. El margen operativo está determinado por el margen bruto y el porcentaje de gastos de operación. De otra parte el Costo Promedio Ponderado de Capital depende del costo de las fuentes de financiamiento, deuda y patrimonio y la estructura de capital de la empresa. Para permitir una descripción gráfica del conjunto de relaciones y la dependencia existente entre las variables se exhibe la gráfica No. 1, donde se explican los factores que inciden en la rentabilidad operativa.
Los árboles de decisión constituyen un instrumento de análisis que permite en principio expresar de forma gráfica, y posteriormente, bajo una esquematización matemática, los diferentes caminos, variables, causas y efectos susceptibles de materializarse como producto de las acciones derivadas por los individuos participantes, no obstante de reconocer en todo caso, que bajo condiciones de incertidumbre y de riesgo, convergen en cada fase elementos de tipo estocástico o aleatorio (Berlanga, Rubio y Vilà, 2013).
Ahora considérese un ejemplo típico en el cual tres individuos presentan intereses en conflicto: pretenden apostar una moneda lanzándola dos veces y anticipando su resultado. Las posibilidades se exhiben en el gráfico No. 2.
Todos los posibles resultados obtenidos a partir de dos lanzamientos consecutivos de una moneda, constituyen los elementos del espacio muestral que, si se denomina como A, será igual a {Sello, Sello; Sello, Cara; Cara, Sello; Cara, Cara} o más sintéticamente a partir de sus iniciales: A= {SS, SC, CS, CC}. La idea es que el primer participante del juego se queda con la moneda si obtiene de forma consecutiva Sello-Sello. El segundo jugador ganará si obtiene la combinación Cara-Cara. Finalmente, el tercer participante resulta ganador si obtiene una combinación no coincidente en el resultado, es decir Cara-Sello o en su defecto, Sello-Cara.
La teoría más simple de probabilidades manifiesta que, si un experimento con un número finito de posibilidades, tal y como aparece en el espacio muestral A, pretende concebir uno de esos eventos, el cálculo de la probabilidad, es decir, la posibilidad de ocurrencia de un fenómeno, se halla determinada por el cociente existente entre el número de posibilidades esperadas sobre la totalidad de casos posibles. En términos matemáticos:
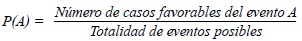
La probabilidad del primer participante se define como la posibilidad de obtener la combinación SS dentro del total de combinaciones factibles que, equivalen al universo A y que está compuesto por cuatro elementos, asé que su valor de probabilidad será:
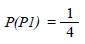
De la misma forma, la probabilidad del segundo jugador será equivalente a la posibilidad de alcanzar el evento CC dentro del total de eventos factibles considerados en el universo A, es decir cuatro, con lo anterior la probabilidad de obtener ganancia para el segundo participante es:
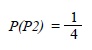
Finalmente, si no se considera un estricto orden de resultados, sino la combinación de los mismos, el tercer participante puede obtener el resultado SC o CS que, implica dos posibilidades lógicas dentro del conjunto de eventos factibles del universo A, lo que implica que el valor de probabilidad, en este caso sea:
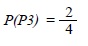
En consecuencia, el resultado deseado en términos de probabilidad será mayor para el jugador 3, que a diferencia de los jugadores 1 y 2 cuyo porcentaje de probabilidad equivale al 25% para cada uno, obtiene una probabilidad total del 50%.
El tema de los árboles de rentabilidad financiera supone la existencia de un conjunto de factores relacionados e interrelacionados de forma permanente y continua en diferentes espacios de tiempo, la dificultad más relevante al analizar este tipo de problemas es que el estudio de un evento supone un “congelamiento impreciso de la realidad”, en otras palabras, la información financiera captura un instante, un punto del tiempo y lo que detenemos bajo la mirada de un fotograma en realidad es una película en continuo movimiento. Este factor por supuesto, tiene como su más conocido talón de Aquiles, el hecho de que mediante una mirada estática del fenómeno se presume una inferencia válida para su óptica dinámica.
Una dificultad adicional estriba en la suposición de un evento totalmente determinístico, esto es que la rentabilidad, el costo o la generación de valor misma, constituyen situaciones dadas como consecuencia de una mecánica no estocástica. Lo anterior implica que la rentabilidad constituye el efecto de decisiones concretas bajo un ambiente de certidumbre y donde basta con aplicar una serie de movimientos en las variables claves para obtener el resultado deseado. La principal diferencia existente entre los árboles de decisión y los árboles de rentabilidad reside precisamente, en que mientras los primeros suponen que un evento histórico puede explicarse de forma determinística, mientras los segundos sugieren que un evento futuro puede presentarse como el resultado de un conjunto de factores de naturaleza probabilística.
La construcción de árboles de decisión se basa en la teoría de juegos (Ferro y Peña, 2002), que constituye un instrumento de análisis cuando intervienen intereses en conflicto entre los agentes económicos. Al respecto Monsalve y Arévalo sostienen que “la forma más común de ilustrar un juego en forma extensiva es mediante un diagrama de árbol. Cada punto posible de una distribución del árbol lo llamamos nodo. Por convención, y para saber dónde comienza el juego, al nodo inicial se le representa con un círculo vacío, y todos los nodos siguientes se presentan como círculos llenos. Las ramas que parten de un nodo son las diferentes acciones disponibles al jugador en ese momento. Cada rama a su vez, conduce a otro nodo. Si no existen ramas que partan de cierto nodo a éste se le llamará nodo terminal y allí se asignarán los pagos de los jugadores” (Monsalve y Arévalo, 2005: 86).
Hacía la construcción de árboles de decisión financiera
La incorporación de los árboles de decisión a la teoría financiera ha sido expresada con especial entusiasmo por el profesor Aswath Damodaran quien señala que convencionalmente “el riesgo de un activo o de una empresa tiende a encapsularse en un número, tras utilizar altas tasas de descuento o bajos cash flow. Además, su cálculo suele requerir asumir ciertos supuestos (la mayoría irreales) acerca de la naturaleza de ese riesgo. Para afrontar este problema, se puede considerar una forma diferente y potencialmente más informativa de valorar y presentar el riesgo de una inversión. Se podría aportar información respecto al valor de un activo (inversión) bajo distintos resultados, o al menos subconjuntos de esos resultados. Y esto es lo que se hace con los árboles de decisión. Este enfoque es posiblemente el más completo para afrontar el riesgo discreto” (Damodaran, 2014).
Como se ha señalado en este documento, la denominada teoría financiera tradicional considera que el manejo de indicadores y las relaciones entre variables comprometidas en el cálculo de los mismos, constituye una herramienta suficiente para explicar los fenómenos de una empresa o mercado. Sin embargo, fenómenos como una noticia inesperada, una guerra o simplemente externalidades propias del entorno como por ejemplo, la presencia de factores de naturaleza socio-cultural, tienen una importante incidencia y la aplicación árboles de decisión precisa ser una herramienta que permite anticipar una serie de escenarios posibles y los mecanismos de acción necesarios para tratarlos.
“Los árboles de decisión también son útiles, porque no sólo permiten considerar el riesgo en cada una de las etapas sino que te ayudan a diseñar la mejor respuesta, dado un resultado determinado (si ocurre x, habría que hacer z). Vincular acciones y opciones a los resultados de eventos inciertos, a través de árboles de decisión, permite a las empresas considerar cómo actuar hoy ante riesgos y circunstancias diferentes. Como consecuencia, las empresas están preparadas para cualquier resultado que pueda suceder, y así, no verse sorprendidas” (Damodaran, 2014).
La aplicación de herramientas computacionales en el análisis de decisiones económicas, financieras, gerenciales constituye un factor que goza de creciente aceptación esencialmente por su maniobrabilidad en el estudio de relaciones e interrelaciones cuya complejidad en la elaboración de cálculos, simulaciones, pronósticos difícilmente podría llevarse a cabo con la precisión y agilidad de un ordenador y de un software especializado. Ejemplos de lo anterior son los programas Gretl, Eviews, stata, statgraphics, smartfolio entre otros. Concretamente WinQSB y Spss se presentan como instrumentos que permiten efectuar muestreo, programación dinámica, proyecciones, teoría y sistemas de inventarios, programación de jornadas de trabajo, procesos y cadenas de Markov, planificación de recursos, modelado de redes, programación no lineal, PERT y CPM, programación cuadrática y árboles de decisión, entre otras posibilidades.
El modelo propuesto se basa en el hecho de que las decisiones de inversión serán tomadas hacía el futuro y en consecuencia, el punto de arranque implica las diferentes opciones de los individuos y en adelante, la simulación de posibilidades a las que, deberá hacer frente en cada nueva etapa del proceso de decisión. Por ejemplo, un inversionista podría estar interesado en aumentar para los próximos cinco años la productividad de los activos operativos. Para ello, debe decidir si sus esfuerzos estarán enfocados en la productividad del capital de trabajo operativo o la productividad del capital fijo, o una opción que combine estos dos elementos según sus preferencias. Además el inversionista debe pensar si el aumento de la productividad de los activos operacionales bastará para incrementar la rentabilidad de la actividad productiva.
Probablemente el agente decisor puede suponer una estrategia paralela basada en generar un estímulo para el mejoramiento del margen de operación, no obstante esta vía paralela de análisis supone que deberá decidir entonces la combinación de esfuerzos requerida para tal fin y su correspondiente asignación en el margen bruto o en los gastos operativos. La suma de las diferentes opciones de combinación entre las medidas que pretenden simular el comportamiento de la rentabilidad, permite la comprensión de varios escenarios y sus potenciales políticas de trabajo. El esquema propuesto en esta metodología se propone de manera gráfica así:
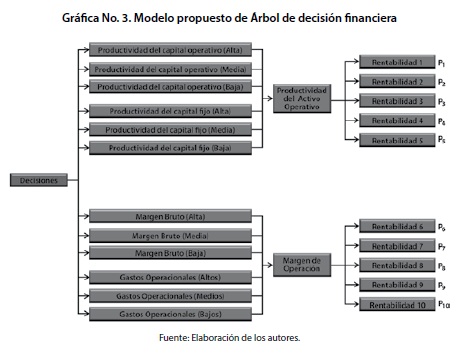
La relevancia de la modelación financiera efectuada a través de los árboles de decisión posibilita advertir que existen alternativas diversas que a su turno implican la instantánea generación de diferentes escenarios. Por ejemplo, si una empresa pretende incrementar sus niveles de rentabilidad hacia el futuro, puede considerar en tiempo presente una amplia gama de situaciones que debe advertir, v. gr. que la productividad del capital operativo sea baja, mientras que la productividad del capital sea alta y que al mismo tiempo el margen bruto sea medio y los gastos operacionales sean bajos. Todas esas posibles combinaciones probabilísticas conducen a la existencia de escenarios probabilísticos para la productividad del activo operativo y el margen de operación, lo que finalmente origina una amplia cantidad de escenarios para la rentabilidad a los que el inversionista y la empresa deben hacer frente mediante la anticipación de política económica o financiera.
El gráfico 4 presenta de forma más concreta, la cantidad de escenarios que una empresa puede advertir, como consecuencia de productividades del activo operativo esperadas, que en efecto, dependen a su vez, de las decisiones suscitadas en la productividad del capital operativo. Aun cuando lo anterior, puede pretender un cambio temporal en la forma de analizar el comportamiento de la rentabilidad o, dicho de otra forma, sugerir un estudio desafiante enfocado hacia el futuro bajo la premisa de considerar las implicaciones venideras experimentadas como fruto de decisiones presentes, es relevante considerar tres aspectos que no pueden pasar inadvertidos frente al tratamiento teórico y de modelación para el estudio de esta clase de fenómenos económicos y financieros, i. las alternativas de decisión ii. Sus probabilidades de ocurrencia asociadas y iii. Las consecuencias de un evento, lo que se tratará en breve.
Arboles de decisión
Un árbol de decisión se define como una herramienta analítica para la selección, estructuración y evaluación de problemas bajo un ambiente de incertidumbre, permite además evaluar planes de acción, efectuar valoración de consecuencias, obtener cálculo de probabilidades y establecer simulaciones. La construcción de árboles de decisión se basa en la existencia de escenarios donde los agentes económicos actúan interactiva y consecutivamente, lo que la diferencia del análisis estático basado en escenarios donde los eventos de estudio se sucedían simultáneamente. A su vez, implican un análisis dinámico basado en la sucesión de eventos consecutivos donde el conjunto de acciones y decisiones futuras se determina por acciones y decisiones presentes, originando precisamente la necesidad de reflejar dentro de un árbol de decisión las consecuencias de eventos probables encaminados hacia el futuro.
Para la elaboración de estos árboles es necesario contar de una parte, con las alternativas de decisión existentes, en segundo término, con los eventos probabilísticos asociados a dichos procesos de decisión y su secuencia que, constituyen el conjunto de sucesos que no se controlan y que presentan incertidumbre y finalmente las consecuencias económicas relacionadas con las posibles decisiones asociadas a los eventos probabilísticos. La secuencia del proceso de decisión que permite articular las decisiones y sus resultados en diferentes escenarios viene establecida por la introducción de nodos de decisión y nodos probabilísticos, cuyo resultado se refleja en los nodos terminales (Cardona, 2004).
En primer término, la construcción de un árbol de decisión exige la definición de un problema, y especialmente, de identificar cuáles son las decisiones que se desean evaluar. Como segundo paso, es necesario estructurar la secuencia de fases que implican cada una de las decisiones establecidas. Naturalmente, una fase posterior debe resolver el árbol mediante valores esperados y selección de una estrategia basada en criterios de maximización o minimización. Adicionalmente una etapa del proceso se detiene en examinar la sensibilidad de uno o varios factores, la forma en que interactúan entre sí y por último, bajo los resultados alcanzados se toma una decisión. El mentefacto que describe este proceso es un diagrama de influencia. En el mismo se exponen las relaciones de causalidad entre las variables críticas, variables no controlables, rutas, y nodos (Cardona, 2004).
En la gráfica 5 es posible advertir un diagrama de influencia que representa el árbol de decisión. En el mismo se establecen tres tipos de nodos, los nodos de decisión; los nodos de probabilidad y finalmente, los nodos terminales en triángulos. Los primeros comprometen una actividad deliberada como estudiar una maestría, aceptar una propuesta laboral, salir de viaje, comprar maquinaria, reducir los costos operativos, capacitar empleados, entre otros. Los segundos involucran sucesos probables que están sujetos situaciones de riesgo e incertidumbre como por ejemplo, enfermarse en la fecha de una evaluación, estabilidad laboral, accidentes de tránsito, aparición de nuevas tecnologías, etc. Por último, los nodos terminales expresan los resultados de un proceso, también denominados consecuencias económicas. Las secuencias se conectan a través de rutas que permiten comprender las relaciones de causa-efecto entre las variables.
Una de las convencionales dificultades conferidas al análisis financiero tradicional, estriba en considerar el diagnóstico de los registros históricos como el principal instrumento para la toma de decisiones. No obstante de que la teoría económica había advertido, en principio con John F. Muth (1961) y luego con Robert Lucas (1972), el concepto de expectativas racionales que, a la postre señala la relevancia no solo de la información histórica sino de las expectativas acerca del futuro, basadas desde luego, en información confiable. Sin desconocer la relevancia de los instrumentos analíticos que examinan el comportamiento histórico, así como las relaciones experimentadas por un conjunto de variables, un juicio objetivo de los fenómenos naturales y sociales evidenciados no puede pasar por alto la necesidad de emplear la simulación de eventos probabilísticos antes de que se conviertan en hechos efectivos y sea imposible interactuar en estos para conducirles a un resultado deseable.
El presente artículo se centra en el diseño de árboles de decisión, caracterizados esencialmente por el estudio de criterios de tipo probabilístico. En ese orden de ideas a manera de ejemplo, se plantea un caso en que se comienza identificando como problema central la decisión concreta de inyectar recursos en una cartera de títulos valores o, por el contrario no invertirlos. Para efectos prácticos, el nodo de decisión representado en el Start, describe la existencia de dos nodos de incertidumbre definidos como Invertir y no Invertir correspondientemente. Del primer nodo, que implica a su vez la posibilidad de invertir, se desprenden dos nodos terminales que se relacionan con la existencia de obtener una alta o baja rentabilidad. De otra parte, se supone que un agente económico que no esté dispuesto a invertir en la cartera de acciones, no compromete ni pérdidas ni ganancias por su decisión; aun cuando en términos prácticos, en este último caso existe un costo de oportunidad latente.
La lectura de un árbol de decisión se lleva a cabo a partir de asegurar unas condiciones de rentabilidad en el portafolio tales que, evalúen la decisión de invertir en escenarios diversos y factibles. Así por ejemplo, si los rendimientos de un portafolio, dada una probabilidad estadística asociada son superiores a las consecuencias económicas de no invertir, conducen indefectiblemente a redefinir el proceso de toma de decisiones y concentrarlo en la inyección de recursos. Las combinaciones de probabilidad originan tantos escenarios como es posible, no obstante, en este apartado se han ejemplificado tres escenarios convencionales, el primero de alta probabilidad de rendimiento, el segundo basado en bajas probabilidades de rendimiento y finalmente, un escenario de probabilidades moderadas.
Aplicación de los árboles de decisión a una cartera de inversiones en Colombia
Para el desarrollo de una aplicación de los árboles de decisión fue necesario diseñar un portafolio de inversión en títulos de renta variable de la Bolsa de valores de Colombia durante el periodo comprendido entre el 12 de mayo de 2011 hasta el 31 de diciembre de 2013. La composición de la cartera optimizada mediante la teoría de Markowitz, es decir, optimizando la relación rentabilidad-riesgo mediante el modelo de media varianza produjo una matriz de riqueza constituida por una asignación del 44% para Banco de Bogotá, 29.49% para Isagen, 20.76% para la Corporación Financiera de Colombia, 2.57% para el Grupo Nutresa, 2.45% para Celsia y 0.73% para Almacenes Éxito.
Considerando la composición de la cartera y su rendimiento anualizado estimado de 10.33% y el valor del riesgo de portafolio anualizado equivalente a 9.77%, fue posible utilizar el teorema expuesto por Pafnuti Chebyshov para determinar valores máximos y mínimos dentro de los cuales oscila el rendimiento de una cartera que se desprenden de adiciones y restricciones graduales de desviaciones estándar basadas en niveles de confianza del 68%, 98% y 99,7%. Los resultados del proceso se ilustran a continuación:
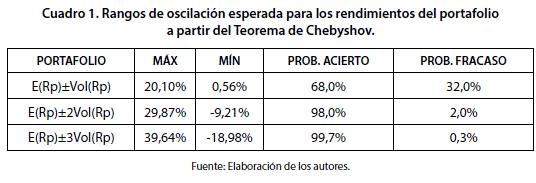
Una vez establecidos los intervalos de oscilación, se procede a tomar aquel que represente mayor nivel de confianza, sin que para efecto de predicción puntual existan implicaciones relevantes, en consecuencia se esperará un valor de 10,33% en el escenario estable, compatible con el resultado de optimización de cartera mediante programación en Solver y sobre su riesgo asociado, un escenario favorable de rentabilidad conjunta equivalente a 39,64% y, un escenario desfavorable donde el rendimiento del portafolio es de -18,98%.
Construcción de árboles de decisión financiera en Risk Simulator
Para la construcción de los árboles de decisión se utilizó el programa RISK SIMULATOR que posibilita la identificación, la medición y valoración del riesgo en proyectos de inversión y permite la simulación y generación de escenarios soportados en diagramas de influencia. El software es utilizado ampliamente para elaborar pronósticos, control de calidad y análisis de sensibilidad.
Una vez planteado el mentefacto o diagrama de influencia se procede a abrir el programa RISK SIMULATOR que, en esencia constituye un complemento de Excel direccionado al tratamiento de análisis de riesgo. Para acceder al instrumento, el usuario debe dirigirse dentro del menú central a la opción “Simulador de Riesgo” y precisar dentro de ella el componente de construcción y evaluación de árboles de decisión denominado “ROV Decision Tree”.
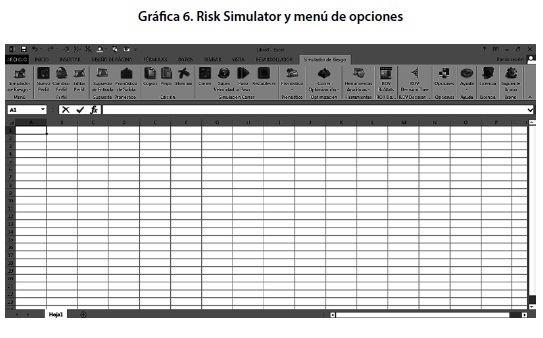
En seguida el programa permitirá la apertura de una nueva ventana denominada “ROV Visual Modeler- Árbol de decisiones” en el cual, por defecto, aparecerá el nodo de arranque o “Start”.

En el menú central de ROV visual modeler- árbol de decisiones, el usuario debe elegir la opción “insertar” y en el submenú deberá elegir los nodos correspondientes al problema particular que desea resolver, que como se explicó anteriormente se clasifican como nodos de decisión, nodos de incertidumbre y nodos terminales. Si se han introducido por ejemplo, dos nodos de incertidumbre, es posible personalizar cada uno de ellos haciendo click y asignándoles un nombre, tal y como se expresa a continuación.
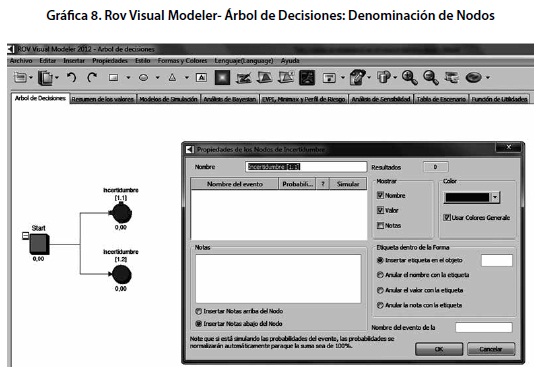
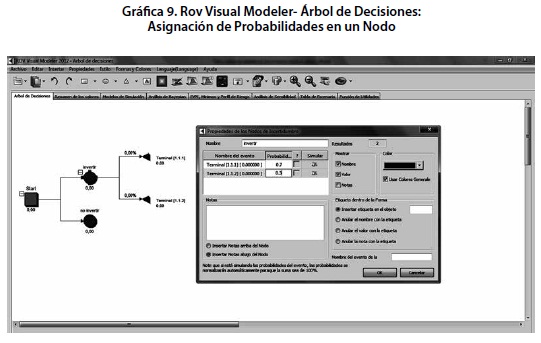
Los valores de 0 que se ubican en la parte inferior de cada nodo corresponden a los valores que hasta el momento describen cada una de las opciones y que, en efecto se resolverán en el nodo de decisión. A continuación, sobre el primer nodo de incertidumbre se introducen dos nodos terminales. En seguida, si se hace click nuevamente sobre el primer nodo “Invertir” es posible establecer el valor de probabilidad correspondiente a los dos nodos que de él se desprenden, considerando, desde luego que la suma de probabilidades debe ser igual al 100% o la unidad. En este caso, si se tiene en mente la constitución de un escenario optimista se establece de manera deliberada que la probabilidad del primer nodo terminal será del 70% (digitado como 0.7) y la probabilidad del segundo nodo terminal abarcará el 30% restante.
Para finalizar, es relevante incorporar a los nodos terminales su denominación y valor esperado, que en este caso se asigna para rentabilidades altas el valor de 39,64% basado en el intervalo superior de Chebyshov al 99,7% de confianza y, rentabilidades negativas de 18,98%.
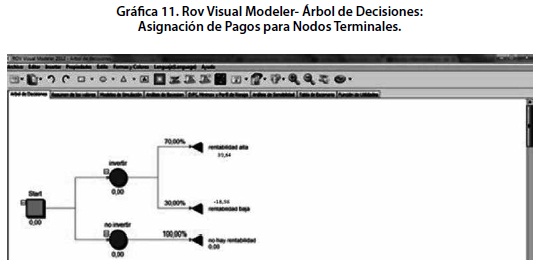
Si se considera que de la opción de no invertir se desprende un nodo terminal denominado “no hay rentabilidad” su valor será de 0% y su probabilidad asociada del 100%. Finalmente, el árbol de decisión propuesto se plantea así:
La resolución del árbol de decisión supone simplemente un resultado de suma producto entre la probabilidad asignada por escenario y el valor establecido para los nodos terminales. El proceso desarrollado a través de RISK SIMULATOR se efectúa eligiendo el menú CORRER y señalando en el recuadro de “Ejecutar opciones” se activan las opciones de Ejecutar la simulación”, “Valor de Semillas”, “Ejecutar la gráfica en vivo en la cuadro del árbol” y “Resaltar la trayectoria con el valor máximo”. Finalmente se presiona la opción “Ejecutar” y automáticamente RISK SIMULATOR calcula el valor esperado y compara cuál de las opciones es la mejor resaltando la rama que constituye la alternativa más conveniente.
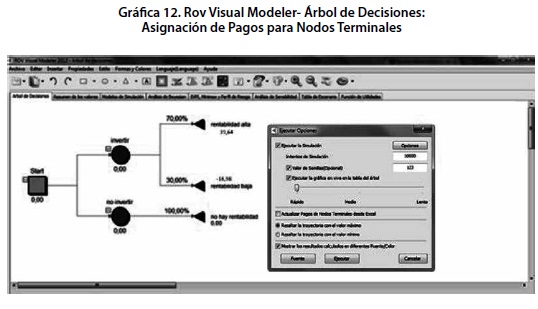
El resultado debe conducir a la generación del primer escenario. Para obtener las simulaciones de escenarios diferentes basta con cambiar la proporción de probabilidades existente en los nodos terminales.
Resultados y análisis de árboles de decisión
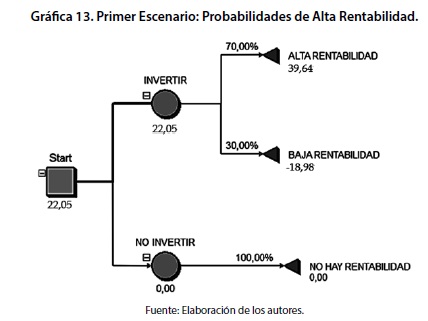
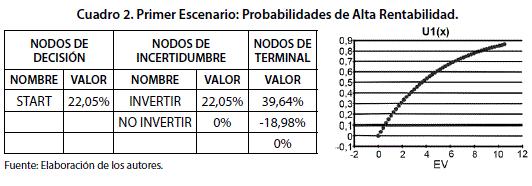
El primer escenario supone un valor esperado de rendimiento correspondiente a 22,05% que se produce como resultado de una probabilidad estadística del 70% sobre la ocurrencia del fenómeno de alta probabilidad combinado con una probabilidad del 30% asociado al evento de baja rentabilidad. El análisis vinculado con este árbol permite dimensionar un resultado aproximado al derivado de la optimización del modelo de media-varianza planteado por Markowitz y que bajo análisis no determinístico es superior a la opción de no invertir. Por consiguiente y en línea con los diagnósticos elaborados en capítulos anteriores, el portafolio de inversión resulta atractivo en un escenario optimista.
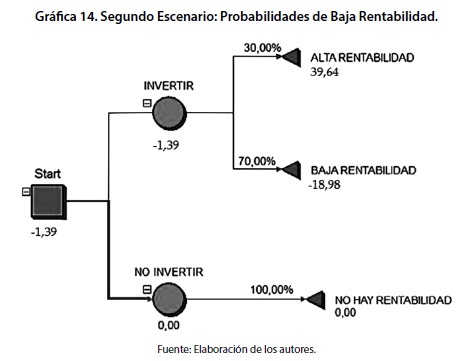

En el segundo escenario, la cartera de inversión exhibió un valor esperado de rendimiento negativo correspondiente a 1,39% como resultado de una probabilidad estadística del 30% alta rentabilidad combinada con una probabilidad del 70% vinculada a la posibilidad de baja rentabilidad. Adicionalmente el resultado de 1,39% es inferior a la opción de no invertir. En consecuencia, el portafolio de inversión no resiste satisfactoriamente un escenario adverso.
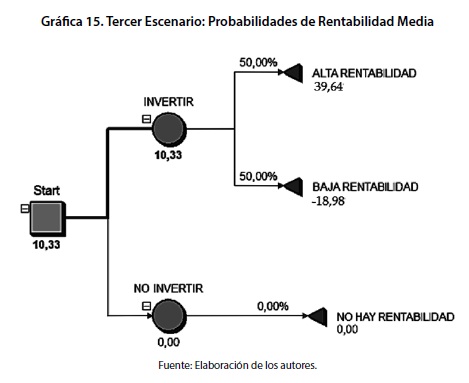
El tercer escenario sitúa al portafolio de inversión con un valor medio de rendimiento equivalente a 10,33%, producto de una combinación de probabilidades del 50% para los eventos de alta rentabilidad y baja rentabilidad. El resultado se basa en la ocurrencia de las aplicaciones de Markowitz y por consiguiente, implica que en el escenario probable las conclusiones obtenidas en el análisis optimizado de media varianza se aplican satisfactoriamente.

CONCLUSIONES
El primer escenario supone un valor esperado de rendimiento correspondiente a 22,05% que se produce como resultado de una probabilidad estadística del 70% sobre la ocurrencia del fenómeno de alta probabilidad combinado con una probabilidad del 30% asociado al evento de baja rentabilidad. El análisis vinculado con este árbol permite dimensionar un resultado superior al derivado de la optimización del modelo de media-varianza planteado por Markowitz y que bajo análisis no determinístico es favorable con respecto a la opción de no invertir. Por consiguiente y en línea con los diagnósticos elaborados en capítulos anteriores, el portafolio de inversión resulta atractivo en un escenario optimista.
En el segundo escenario, la cartera de inversión exhibió un valor esperado del rendimiento correspondiente a -1,39% como resultado de una probabilidad estadística del 30% asociada a la ocurrencia del fenómeno de alta rentabilidad combinada con una probabilidad del 70% vinculada a la posibilidad de baja rentabilidad. En este caso el resultado es muy inferior al originado en la optimización del modelo de Markowitz. Adicionalmente el resultado de -1,39% es inferior a la opción de no invertir. En consecuencia, el portafolio de inversión no resiste satisfactoriamente un escenario adverso.
El tercer escenario sitúa a portafolio de inversión con un valor medio de rendimiento equivalente a 10,33% producto de una combinación de probabilidades del 50% para los eventos de alta rentabilidad y baja rentabilidad. El resultado se basa en la ocurrencia de las aplicaciones de Markowitz y por consiguiente, implica que en el escenario probable las conclusiones obtenidas en el análisis optimizado de media varianza se aplican satisfactoriamente.
REFERENCIAS
1. ALEXANDER, Gordon J.; SHARPE, William F y BAILEY, Jeffery V. (2003). Fundamentos de Inversiones: Teoría y Práctica. Prentice-Hall, México.
2. BERLANGA, Vanesa, RUBIO María José y VILÀ Ruth (2013). Cómo aplicar árboles de decisión en SPSS. Revista d’Innovació i Recerca en Educació. Universitat de Barcelona. Institut de Ciències de l’Educació. Vol. 6, núm. 1, enero.
3. BERMEJO IGLESIAS, Antonio; TORRES PRUÑONOSA, José y MASFERRER LLAVINÉS, Núria (2009). “La utilización de los modelos ARIMA en la estimación del precio de acciones: una aplicación preliminar”. En: F.J. COSSÍO SILVA. Administrando en entornos inciertos. Escuela Superior de Gestión Comercial y Marketing, ESIC. España.
4. BOLLERSLEV, T., (2001), “Financial Econometrics: Past Developments and Future Challenges,” Journal of Econometrics, Vol. 100, pp. 41-51.
5. CARDONA HERNÁNDEZ, Paola Andrea (2004). Aplicación de árboles de decisión en modelos de riesgo crediticio. Revista Colombiana de estadística. Volumen 27 No. 2. Diciembre.
6. DAMODARAN, Aswath (2014). “Uno de los mayores errores es asumir que el crecimiento de una compañía es gratis o muy barato”. Entrevista concedida a Javier García para el portal Sintetia.com el 13 de Enero de 2014. Consultada el 10 de febrero de 2015. Disponible en: http://www.sintetia.com/aswath-damodaran-stern-finance/?utm_content=buffera2ae1&utm_medium=social&utm_source=twitter. com&utm_campaign=buffer.
7. ENGLE, R.F. (2001), “Financial Econometrics: A New Discipline with New Methods,” Journal of Econometrics, Vol. 100, pp. 53-56.
8. FERRO, Jorge Luis y PEÑA, Darío (2002). Juegos y Finanzas. Odeón. Borradores de investigación. Universidad Externado de Colombia, Bogotá, Diciembre. Pp. 149-160.
9. GUJARATI, Damodar N. y PORTER, Dawn C. (2010). Econometría. Mc Graw-Hill. México. 921p.
10. HANKE, John E. y WICHERN, Dean W. (2010). Pronósticos en los Negocios. Pearson. México.
11. HERNÁNDEZ RAMÍREZ, Enrique. “Neurofinanzas: Cuando las decisiones financieras no son racionales”. En: TEC empresarial. Vol. 4. No. 3. Costa Rica, 2010. Pp. 21-30.
12. MONSALVE, S. y ARÉVALO, J. (2005). Un curso de teoría de juegos clásica. Universidad Externado de Colombia.
13. OLAYA PARDO, Ana María (2002). Las finanzas en la frontera del conocimiento. Economía. Borradores de Investigación. Universidad del Rosario. No. 33. Bogotá, Diciembre.
14. ORDÓÑEZ DE PABLOS, Patricia (2000). Importancia estratégica de la medición del capital intelectual en las organizaciones. Disponible en: http://www.injef.com/revista/empresas/pop_991217.htm.
15. RÍOS INSÚA, David; RÍOS INSÚA, Sixto; MARTÍN JIMÉNEZ, Jacinto y JIMÉNEZ MARTÍN, Antonio (2009). Simulación: Métodos y Aplicaciones. Alfaomega. México.
16. SMITH, Adam (1997). Investigación sobre la Naturaleza y Causas de la Riqueza de las Naciones. Fondo de Cultura Económica. México.
17. TARZIJÁN, J. y R. PAREDES (2012): Organización Industrial para la Estrategia Empresarial, Pearson Education-Prentice Hall, Buenos Aires.
18.TAUCHEN, G. (2001), “Notes on Financial Econometrics,” Journal of Econometrics, Vol. 100, pp. 57-64.
19. VITORIANO, Begoña (2007). Teoría de la Decisión: Decisión con Incertidumbre, Decisión Multicriterio y Teoría de Juegos.