LA FUNCIÓN DE PRODUCCIÓN COBB-DOUGLAS EN EL ECUADOR*
THE PRODUCTION FUNCTION COBB-DOUGLAS IN THE ECUADOR
A FUNÇÃO DE PRODUÇÃO COBB-DOUGLAS NO ECUADOR
Por: Xavier Fernando Briones Bendoza1, Leobaldo Enrique Molero Oliva2, Oscar Xavier Zamora3
1Maestría en Administración de Empresas y Marketing por la Universidad de Guayaquil en convenio con la Universidad de Guadalajara. Docente en la Universidad Eloy Alfaro de Manabí (ULEAM). Email: reivaxlia@hotmail.com, Ecuador.
2Maestría en Economía, mención Macroeconomía y Política Económica por la Universidad del Zulia, Docente Escuela de Economía, Universidad del Zulia. Email: lmolerooliva@gmail.com, Venezuela.
3Maestría en Tributación y Finanzas. Docente de la Facultad de Administración de Empresas en la Universidad Laica Eloy Alfaro de Manabí (ULEAM). Email: osc4200@hotmail.com, Ecuador.
Recibido: 19 de marzo de 2018 Aprobación
definitiva: 3 de octubre de 2018
*Este artículo es resultado de una investigación preliminar preparada para el Doctorado en Ciencias Económicas de la Universidad del Zulia. Los interesados en el acceso a las bases de datos y códigos computacionales para la verificación del modelo final por favor escribir a los correos de los autores. Agradecemos los comentarios y sugerencias del Profesor Bladimir Pozo. Los hallazgos, interpretaciones y conclusiones pertenecen a los autores y no representan los puntos de vistas de las instituciones en las cuales participan como profesores y estudiantes. Finalmente, como es usual los errores restantes y omisiones son de responsabilidad exclusiva de los autores.
Resumen
El objetivo principal de este trabajo es analizar el comportamiento de la elasticidad del producto ante cambios en los dos factores de producción: capital y trabajo, en una función de producción con rendimientos constantes a escala. Para ello, se discute el marco teórico de acuerdo a la revisión bibliográfica efectuada y mediante algunos modelos econométricos se estima una función con propiedades neoclásicas como la función Cobb-Douglas para el caso del Ecuador en el período 1950-2014. En el modelo teórico la elasticidad es otra forma de presentar las participaciones de cada insumo dentro del producto, y en competencia perfecta son iguales a las remuneraciones recibidas en la distribución del ingreso. Las estimaciones efectuadas arrojan resultados que indican una participación del capital dentro del producto que oscila entre 0,60 y 0,70, es decir, esto es la elasticidad del producto respecto al capital, según varias regresiones a corto y a largo plazo de la función de producción agregada e intensiva. Los resultados hallados coinciden con las estimaciones disponibles para un amplio grupo de países en vía de desarrollo.
Palabras claves: función de producción, rendimientos constantes a escala, elasticidad del producto, función Cobb-Douglas, Ecuador.
JEL: C22, D24, E23, E24.
Abstrac
The principal aim of this work is to analyze the behavior of the elasticity of the output before changes in both factors of production: capital and labour, in a function of production with constant returns to scale. For it, the theoretical framework of agreement is discussed to the bibliographical effected review and by means of some econometrics models a function is estimated by neoclassic properties as the function Cobb-Douglas for the case of the Ecuador in the period 1950-2014. In the theoretical model the elasticity is another way of presenting the participations of every input inside the output, and in perfect competition they are equal to the remunerations received in the distribution of the income. The effected estimations throw results that indicate a participation of the capital inside the output that ranges between 0,60 and 0,70, that is to say, this is the elasticity of the output with regard to the capital, according to several regressions to shortly and long-term of the function of added and intensive production. The found results coincide with the available estimations for a wide group of developing countries.
Key words: production function, constant returns to scale, output elasticity, Cobb-Douglas function, Ecuador.
JEL: C22, D24, E23, E24.
Resumo
O principal objetivo deste trabalho é analisar o comportamento da elasticidade do produto antes das mudanças nos dois fatores de produção: capital e trabalho, em função da produção com rendimentos constantes. Para isso, o quadro teórico é discutido de acordo com a revisão bibliográfica realizada e, usando alguns modelos econométricos, uma função com propriedades neoclássicas é estimada, como a função Cobb-Douglas para o caso do Equador no período 1950-2014. En el modelo teórico la elasticidad es otra forma de presentar las participaciones de cada insumo dentro del producto, y en competencia perfecta son iguales a las remuneraciones recibidas en la distribución del ingreso. As estimativas feitas mostram resultados que indicam uma participação capital no produto que oscila entre 0,60 e 0,70, ou seja, esta é a elasticidade do produto em relação ao capital, de acordo com várias regressões de curto e longo prazo da função de produção agregada e intensiva. Os resultados encontrados coincidem com as estimativas disponíveis para um longo grupo de países em desenvolvimento.
Palavras-chave: função de produção, retornos constantes à escala, elasticidade do produto, função Cobb-Douglas, O Ecuador.
JEL: C22, D24, E23, E24.
I. INTRODUCCIÓN
La economía ecuatoriana ha mostrado, recientemente, altas tasas de crecimiento económico. Entre 2000 y 2009 el Ecuador creció a un ritmo promedio de 5,8%, y entre 2010 y 2014 lo hizo a 5,2% en términos per cápita. Estas tasas promedios son las más altas por décadas desde 1950, con excepción del lapso 1970-1979 cuando la economía creció 6,6%. Luego de la década de los ochenta, marcada por el fracaso del modelo de sustitución de importaciones y la crisis de la deuda externa, y la década de los noventa destacada por agudos conflictos políticos internos, otros externos (la guerra con Perú en 1995), e inestabilidad macroeconómica y altas tasas de inflación causadas por vulnerabilidades internas y externas, que conllevaron a un proceso de ajuste macroeconómico y dolarización oficial en 2000 (Ontaneda, 2017: 16), el Ecuador ha retomado la senda del crecimiento, impulsando el ingreso per cápita hacia niveles de ingreso medio.
En ese sentido, es de interés indagar las causas detrás del crecimiento económico del Ecuador, pues el crecimiento tiene importantes implicaciones en los niveles de vida y bienestar humano (Romer, 2012: 8). Un primer paso en esa línea consiste en estimar una función de producción, para conocer las productividades marginales del producto pues, según Weil (2006:54), la proporción del ingreso recibida por los propietarios de los factores es uno de los datos fundamentales cuando se estudia el crecimiento y esas remuneraciones se conocen a través de una función de producción.
Desde el famoso artículo de Charles Cobb y Paul Douglas (Cobb y Douglas, 1928), los economistas han empleado diferentes tipos de funciones de producción, con ciertas propiedades, para analizar el impacto de cada factor sobre el producto. La función brindada por Cobb y Douglas, conocida como función de producción Cobb-Douglas (en adelante CD), permite estimar la elasticidad del producto al capital y al trabajo, los cuales suponiendo competencia perfecta reflejan las productividades marginales de cada factor y, por tanto, sus contribuciones respectivas al producto y participación en el ingreso.
Habitualmente, estas elasticidades o parte del ingreso generado en la producción que es percibida por los propietarios de los factores se pueden conocer por medio de dos alternativas (Monge, 2012: 9). Por una parte directamente de la contabilidad nacional, con la tasas de participación de las remuneraciones del capital y del trabajo en el ingreso, más esta metodología arroja el inconveniente de que parte de los trabajadores lo son por cuenta propia, sobre todo en economías en vías de desarrollo, y no perciben un salario formal, todo lo contrario una amplia parte de los ocupados están en el mercado informal, lo que hace que esos ingresos se contabilicen como ingresos al capital (Aquino y Ramírez, 2017; Monge, 2012: 9; Gollin, 2002: 471). De este modo, la medición de la participación del trabajo presenta dificultades en países de ingreso bajo y medio-bajo (Trapp, 2015).
Por otra parte se puede estimar una función de producción individual para hallar los valores de la elasticidad del producto a cambios en los factores (Astorga y Valle, 2003: 22). Este enfoque implica adoptar una forma funcional de la producción con criterios a priori o basados en hechos estilizados de las economías, y estimar la elasticidad producto-capital y producto-trabajo.
Este trabajo adopta la segunda opción, por lo que el objetivo principal consiste en analizar el comportamiento de la elasticidad del producto ante cambios en los factores, estimando una función de producción CD para el Ecuador durante el lapso 1950-2014. Una de las limitaciones de este trabajo es que no profundiza en la contabilidad del crecimiento, no obstante el mismo puede considerarse un antecedente para futuras investigaciones en este campo. Del mismo modo, el trabajo no considera estimaciones de otros tipos de funciones de producción, como por ejemplo la función CES (constant elasticity of substitution o elasticidad de sustitución constante) (Arrow et al., 1961). No obstante, la función de producción CD sigue siendo válida para recoger la estructura de producción de las economías, tal como lo muestran diversos estudios empíricos para varios países y períodos, de ahí su popularidad entre los economistas (Miller, 2008:1).
II. ASPECTOS FORMALES DE LA FUNCIÓN DE PRODUCCIÓN
La producción con funciones de rendimientos constantes a escala:
Una firma o empresa es alguna entidad que emplea insumos económicos como tierra, trabajo, y capital, para producir cantidades de bienes y servicios para los hogares u otras firmas (Intriligator, 1971: 178), es decir, la empresa tiene como principal actividad convertir factores en producto (Nicholson, 1997). Las decisiones que adoptan las empresas o la economía en su conjunto para alcanzar el objetivo de un nivel de producto, a partir de una dotación de factores productivos, se analizan con un modelo abstracto de producción, formalizado por medio de una función de producción, que muestra la relación tecnológica entre los factores y los productos:
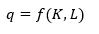 (1)
(1)
Donde q es la cantidad de producción de un determinado bien, producido por la empresa o firma representativa en un período. Se denota con la letra minúscula q, mientras que el uso de Q es para denotar el producto agregado de la economía. Por su parte, K es el stock de capital (maquinarias, herramientas, equipos, edificios), objetos físicos que aumentan nuestra capacidad o hacen el trabajo por nosotros (Weil, 2006:48), producidos en el pasado por una función de producción como la que describimos, y que la empresa o la economía emplean en ese período, L representa el número de trabajadores ocupados en la empresa representativa o, alternativamente, el número de horas de trabajo. El modelo supone que no hay diferencias en la calidad de los factores (son homogéneos), y a veces no considera a las materias primas, lo que es lo mismo, la producción es el valor añadido (Nicholson, 1997). La función simplemente dice que la producción de la firma “representativa” depende del nivel de K y L que se emplee en un período. Conforme a Weil (2006: 50), los factores son productivos, porque su uso aumenta la cantidad de producto que la empresa o la economía pueden obtener, es decir, q es una función positiva y creciente de los dos factores.
Se asume que (1) es continuamente diferenciable y satisface dos axiomas (Intriligator, 1971: 179). El primer axioma relacionado con las productividades marginales de cada factor productivo. Las derivadas parciales del producto respecto a cada insumo conforman un vector de valores positivos 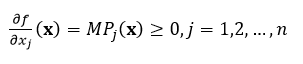 donde
donde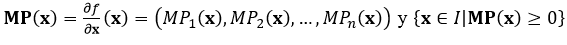 (Intriligator, 1971: 180).
(Intriligator, 1971: 180).
El segundo axioma muestra que las segundas derivadas de la función o derivadas parciales de segundo orden de la función son negativas 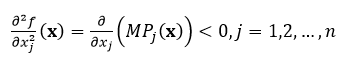 (Intriligator, 1971:180), que se conoce como la hipótesis de los retornos decrecientes: la agregación adicional de más y más de uno de los insumos, manteniendo fijos los restantes, genera disminuciones de la producción total.
(Intriligator, 1971:180), que se conoce como la hipótesis de los retornos decrecientes: la agregación adicional de más y más de uno de los insumos, manteniendo fijos los restantes, genera disminuciones de la producción total.
Dados estos dos axiomas, existe una región relevante definida por 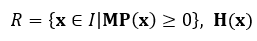 matriz hessiano negativa definida para todo x en R. Intriligator señala que la función de producción es caracterizada en la región relevante por retornos a escala y posibilidades de sustitución (1971: 180). Por retornos a escala la teoría se refiere al comportamiento del producto cuando todos los insumos, capital y trabajo, cambian simultáneamente en la misma proporción. Si todos los insumos son multiplicados por un factor escalar λ entonces
matriz hessiano negativa definida para todo x en R. Intriligator señala que la función de producción es caracterizada en la región relevante por retornos a escala y posibilidades de sustitución (1971: 180). Por retornos a escala la teoría se refiere al comportamiento del producto cuando todos los insumos, capital y trabajo, cambian simultáneamente en la misma proporción. Si todos los insumos son multiplicados por un factor escalar λ entonces 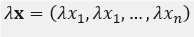 donde λ >0. Si la función de producción exhibe rendimientos constantes a escala una duplicación en ambos factores ocasionará una duplicación del producto .
donde λ >0. Si la función de producción exhibe rendimientos constantes a escala una duplicación en ambos factores ocasionará una duplicación del producto .
Esta característica es muy importante para la aplicación económica que se pretende en este trabajo. Las funciones de rendimientos constantes a escala son homogéneas de grado uno o a veces linealmente homogéneas (Chiang y Wainwrigth, 2006), y su elasticidad de sustitución es constante e igual a 1. Así, la elasticidad del producto sobre cualquier punto en la región relevante es la suma de todas las elasticidades con respecto a los insumos.
De acuerdo a Nicholson (1997: 214), las funciones de producción de rendimientos constantes de escala tienen la interesante propiedad teórica de que la relación marginal de sustitución técnica entre K y L a lo largo de una isocuanta depende solamente del cociente 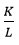 La elasticidad de sustitución σ mide la variación proporcional de K/L en relación con la variación proporcional de la relación marginal de sustitución técnica a lo largo de una isocuanta
La elasticidad de sustitución σ mide la variación proporcional de K/L en relación con la variación proporcional de la relación marginal de sustitución técnica a lo largo de una isocuanta 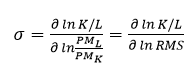 . Por tanto, en el caso de rendimientos constantes de escala, la elasticidad de sustitución de la función es igual a 1, y el parámetro de sustitución es igual a cero. La función de producción en la que σ =1 se denomina función de producción Cobb-Douglas (Nicholson, 1997: 214) y equivale a participaciones constantes de K y L.
. Por tanto, en el caso de rendimientos constantes de escala, la elasticidad de sustitución de la función es igual a 1, y el parámetro de sustitución es igual a cero. La función de producción en la que σ =1 se denomina función de producción Cobb-Douglas (Nicholson, 1997: 214) y equivale a participaciones constantes de K y L.
La función de producción agregada neoclásica y el modelo Solow
El modelo de crecimiento de Solow se basa en una función de producción neoclásica que conserva las propiedades descritas en la sección anterior: 1) presenta rendimientos constantes 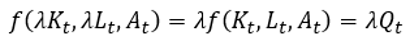 ; 2) la productividad marginal de los factores es positiva, pero decreciente
; 2) la productividad marginal de los factores es positiva, pero decreciente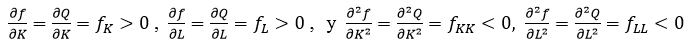 . El Modelo de Solow sigue el caso especial de cambio técnico neutro en el sentido de Hicks (Solow, 1957: 312), por lo que la función de producción toma la forma especial:
. El Modelo de Solow sigue el caso especial de cambio técnico neutro en el sentido de Hicks (Solow, 1957: 312), por lo que la función de producción toma la forma especial:
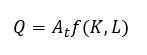 (2)
(2)
Tomando logaritmo y diferenciando totalmente en (2) con respecto al tiempo para obtener la tasa de crecimiento del producto agregado (Romer, 2012: 30; Sala-i-Martin, 2000: 218; Solow, 1957: 312) se obtiene (3). Multiplicando y dividiendo en el lado derecho de la ecuación (3) los términos del primer paréntesis por K y los del segundo paréntesis por L se logra (4):
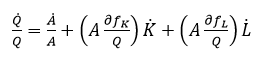 (3)
(3)
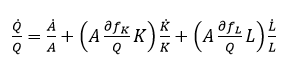 (4)
(4)
En competencia perfecta el producto marginal del trabajo es igual al salario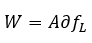 y el producto marginal del capital es igual a su precio de alquiler
y el producto marginal del capital es igual a su precio de alquiler 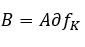 (Sala-i-Martin, 2000: 43). El término
(Sala-i-Martin, 2000: 43). El término 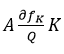 es la participación del capital en el ingreso nacional, mientras que
es la participación del capital en el ingreso nacional, mientras que 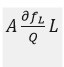 es la participación del trabajo.
es la participación del trabajo.
Denotando 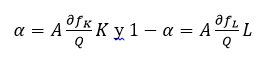 y entonces:
y entonces:
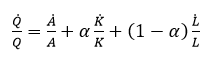 (5)
(5)
Donde α y (1-α ) miden las participaciones del capital y del trabajo, respectivamente, dentro del producto total, y reflejan la parte del producto que corresponde al capital y al trabajo por sus productividades marginales. Esta última expresión provee una descomposición del crecimiento observado entre los componentes asociados con el cambio en los factores productivos y un componente residual para el progreso tecnológico (Romer, 2012: 34). Solow (1957:319) halló que la función CD presenta un mejor comportamiento respecto a otras funciones de producción para estimar el verdadero valor de la contribución del capital al producto, por lo que desde entonces se estiman funciones CD para conseguir una medida de las elasticidades del producto.
La función Cobb-Douglas y las participaciones factoriales
Una de las funciones de producción homogénea más usadas en el análisis teórico y empírico del crecimiento y la productividad es la función Cobb-Douglas (Cobb y Douglas, 1928; Felipe y Adams, 2005: 428):
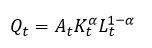 (6)
(6)
Donde Q es el producto total, K y L son las cantidades de insumo capital y trabajo, y 0<α<1. Se puede demostrar con esta función que si se aumentan ambos niveles de capital y trabajo por el factor λ entonces 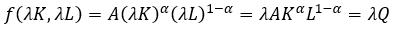 . Esta función cumple las propiedades neoclásicas discutidas antes, particularmente sus derivadas parciales de primer orden son iguales a las participaciones medias del trabajo y el capital en el producto agregado, y las derivadas parciales de segundo orden existen, son continuas y menores que cero (Azofeifa y Villanueva, 1996) . Además, el Teorema de Euler establece para una función linealmente homogénea la siguiente condición (Chiang y Wainwrigth, 2006):
. Esta función cumple las propiedades neoclásicas discutidas antes, particularmente sus derivadas parciales de primer orden son iguales a las participaciones medias del trabajo y el capital en el producto agregado, y las derivadas parciales de segundo orden existen, son continuas y menores que cero (Azofeifa y Villanueva, 1996) . Además, el Teorema de Euler establece para una función linealmente homogénea la siguiente condición (Chiang y Wainwrigth, 2006):
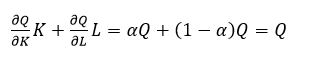 (7)
(7)
De manera que 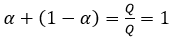 . Esta expresión dice que el valor de una función linealmente homogénea siempre puede expresarse como una suma de términos, cada uno de los cuales es el producto de una de las variables independientes y de la derivada parcial de primer orden respecto a esa variable (Chiang y Wainwrigth, 2006: 385-386). Si se asume que los propietarios de los insumos factoriales cobran por su productividad marginal, entonces
. Esta expresión dice que el valor de una función linealmente homogénea siempre puede expresarse como una suma de términos, cada uno de los cuales es el producto de una de las variables independientes y de la derivada parcial de primer orden respecto a esa variable (Chiang y Wainwrigth, 2006: 385-386). Si se asume que los propietarios de los insumos factoriales cobran por su productividad marginal, entonces 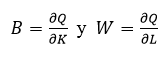 por tanto dada (7):
por tanto dada (7):
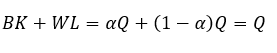 (8)
(8)
En conclusión, en una función con rendimientos constantes a escala, la suma de las elasticidades es unitaria y equivale, en el lenguaje de la distribución, a decir que el producto se agota, o lo que es lo mismo, el ingreso que va al capital y el que remunera al trabajo (1 - α ) son iguales a sus respectivas productividades marginales (Sala-i-Martin, 2000: 43), y su suma equivale a todo el producto:
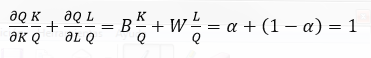 (9)
(9)
De esta forma, estimar una función de producción para medir la elasticidad del producto respecto al capital y al trabajo equivale a contrastar el tipo de rendimientos a escala que la función presenta, y si estadísticamente hablando la suma de las elasticidades no es distinta de uno entonces se puede asumir rendimientos constantes a escala y todo el producto se agota remunerando a los factores productivos. Si se toman logaritmo natural en la función CD se obtiene una forma bastante útil para aplicaciones:
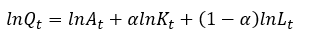 (10)
(10)
Donde es la elasticidad de la producción con respecto a la cantidad de capital y la elasticidad de la producción con respecto a la cantidad de trabajo (Nicholson, 1997:214). Comúnmente en lugar de examinar el producto agregado es más interesante examinar la producción por trabajador en función del capital por trabajador (Weil, 2006: 52), ventaja que proviene del supuesto de rendimientos contantes a escala. Si la función de producción se multiplica por la constante 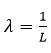 se obtiene la forma intensiva:
se obtiene la forma intensiva:
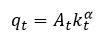 (11)
(11)
Donde 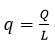 es la cantidad de producción por trabajador que es solo una función de
es la cantidad de producción por trabajador que es solo una función de 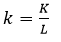 cantidad de capital por trabajador, y de la tecnología. La forma lineal en los parámetros de (11) se obtiene tomando logaritmo:
cantidad de capital por trabajador, y de la tecnología. La forma lineal en los parámetros de (11) se obtiene tomando logaritmo:
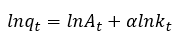 (12)
(12)
III. REVISIÓN DE LA LITERATURA
Las funciones de producción son un componente fundamental de todas las economías (Collard-Wexler y De Loecker, 2016: 2; Ackerberg et al., 2015: 2411; Bellod, 2011). Las características, propiedades y estimaciones de la especificación CD se encuentran en una amplia literatura, sin embargo, también se encuentran perspectivas teóricas y empíricas críticas. Bellod (2011: 16) expresa que la CD es plenamente coherente con la teoría neoclásica de la producción, la distribución y el crecimiento, pero sus supuestos son muy restrictivos e incompatibles con las economías reales; Duffy y Papageorgiou (2000) presentan evidencia sugiriendo que la especificación CD para la función de producción agregada no es válida empíricamente; y Antràs (2004: 26) para el caso de EE UU sostiene que la especificación es engañosa.
A pesar de las críticas, Aiyar y Dalgaard (2009) encuentran que la especificación CD tiene un desempeño razonablemente bueno para ciertos propósitos. Felipe y Adams (2005) presentan reestimaciones de la CD a partir de la data original de Cobb y Douglas (1928) encontrando en varias regresiones resultados muy similares a los obtenidos inicialmente (Felipe y Adams, 2005: 431). Los resultados hallados, bajo la forma lineal de una CD, indican que la hipótesis de rendimientos constantes a escala no puede ser rechazada. La elasticidad del producto al capital y al trabajo fueron 0,233 y 0,751, respectivamente, que permiten verificar el supuesto de que la CD reproduce la participaciones factoriales en el ingreso nacional.
Lo anterior es consistente con el trabajo de Dorta quién halló evidencia de retornos constantes a escala en Venezuela (2006: 20). La estimación muestra una elasticidad producto-capital de 0,55, en promedio, la cual se aproxima bastante bien al comportamiento de la participación del capital en el producto de Venezuela (Dorta, 2006). Recientemente Suárez (2010) brinda estimaciones para la Argentina entre 1975 y 2006. El objetivo de este trabajo consiste en determinar, entre varias estimaciones, la función de producción más apropiada para describir el proceso productivo argentino. Este autor expone que la CD estimada en forma intensiva y en forma directa es una de las funciones de producción obtenidas que mejor logran su cometido (Suarez, 2010:83).
En el caso ecuatoriano resalta el trabajo de Aravena (2010) y Astorga y Valle (2013). El primero no estima econométricamente las elasticidades del producto ante variaciones del capital y del trabajo, sino que asume para todos los países, incluyendo el Ecuador, una participación del capital en el producto igual a 0,4, y una participación del trabajo en el producto igual a 0,60 (Aravena, 2010: 14), mientras que Astorga y Valle estimaron participaciones del capital y del trabajo de 0,61 y 0,39, respectivamente para el período 1988-2002 (2013: 27).
Azofeifa y Villanueva (1996) y Monge (2012) estimaron una función de producción CD para Costa Rica. Azofeifa y Villanueva hallaron resultados que indican una elasticidad producto-trabajo entre 0,42 y 0,62 en las regresiones con constante, y elasticidades menores a 0,35 en las regresiones que no incluyen término constante, por lo cual destacan que la elasticidad producto-capital en todas las regresiones permaneció dentro en un rango menos amplio de valores, y concluyen que la CD es pertinente para describir el caso de Costa Rica. Mientras que Monge (2012: 23) halló una elasticidad producto-trabajo estimada de 0,56. Por último, Elias (1992) reporta una alta elasticidad producto-capital en siete economías latinoamericanas, que contrasta significativamente con la participación del capital en los países industrializados. En ese sentido, una comparación se halla en Barro y Sala-i-Martin, (2004: 439), donde se muestra a partir que la elasticidad del producto al capital es más baja en los países ricos respecto a los países en desarrollo.
IV. METODOLOGÍA ECONOMÉTRICA
El principal propósito de este artículo es estimar una función CD para el Ecuador. Para ello, se emplea la metodología de Mínimos Cuadrados Ordinarios (MCO) en un grupo de modelos uniecuacionales, con base en el enfoque de cointegración y de corrección del error (Engle y Granger, 1987). La especificación econométrica de la ecuación (10) en niveles y tasa de crecimiento son (ecuaciones 13 y 14):
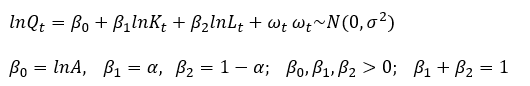 (13)
(13)
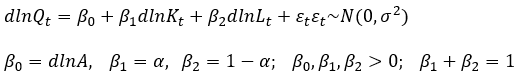 (14)
(14)
Donde se supone que los términos de perturbación aleatoria son variables aleatorias con media cero, varianza constante e independientes en el tiempo. Por su parte, los modelos econométricos de la forma intensiva son:
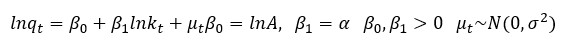 (15)
(15)
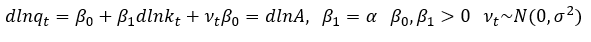 (16)
(16)
En este estudio se utilizan series anuales para 1950-2014 (t= 1,2, …,65). Las variables y series son descritas en la Tabla I. La fuente de los datos primarios es la Penn World Tables 9.0 (PWT). Se efectuaron trasformaciones sobre la base de las series originales, en concreto se construyeron las variables y series producto real agregado por trabajador ocupado q, y el stock de capital bruto por trabajador ocupado k. Así mismo, se efectuaron transformaciones a las series, en efecto se expresaron en logaritmo natural (el término indica el logaritmo natural de la variable), y en tasa de crecimiento, aproximada como la primera diferencia en el logaritmo.
Como paso previo y considerando que las variables son series de tiempo se determinó con las rutinas de Eviews 7 el orden de integración de las variables (ver Tabla II), según las pruebas Dickey-Fuller Aumentada (ADF), Phillips-Perron (PP) y Kwiatkowski-Phillips-Schmidt-Shin (KPSS). Las variables y InQ, InK, InL, Inq y Ink no rechazan la hipótesis nula de raíz unitaria según ADF y PP a cualquier nivel de significancia; sin embargo, las primeras diferencias de todas las series resultaron estacionarias en la mayor parte de las especificaciones de las pruebas ADF, PP y KPSS, con niveles de significancia de 1% y 5%. L a conclusión es que InQ~(1), InK~I(1), InL~I(1), Inq~I(1) y Ink~I(1).
Tabla I
Descripción de variables y series empleadas
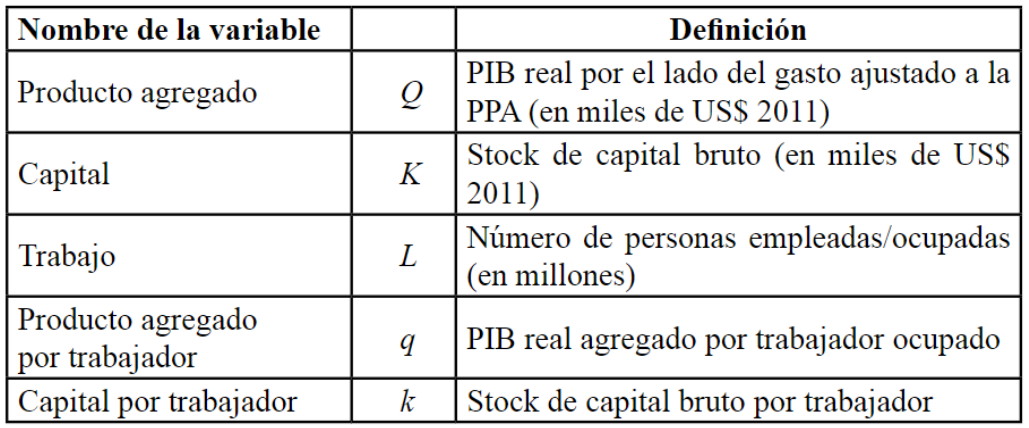
Fuente: PWT 9.0 y cálculos propios (2018) a partir de Eviews 7.
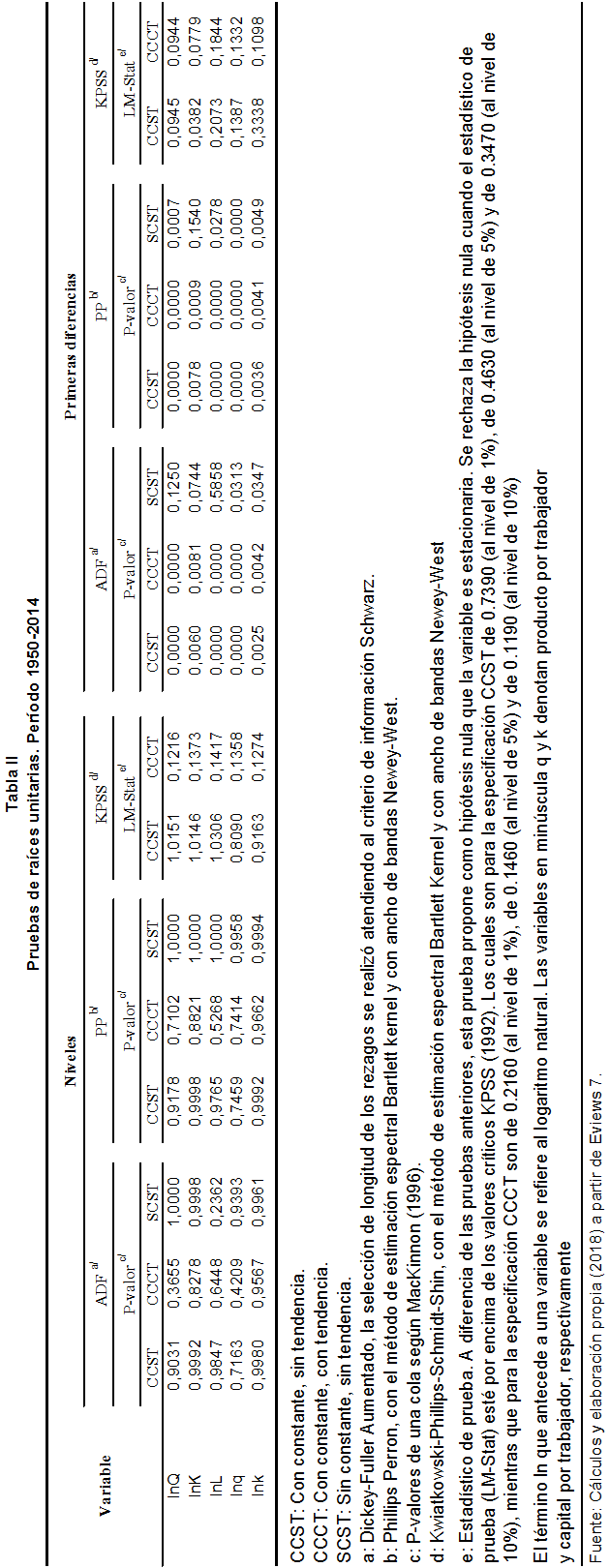
V. RESULTADOS
Estimaciones agregadas:
La Tabla III presenta los resultados en tres estimaciones diferentes de la ecuación (13) de la función de producción agregada sin restricciones. La primera versión incluyó un término constante para recoger la variable de tecnología (InA), los logaritmos de K y L, y tres variables dummy para los años 1974, 1982 y 2000. La segunda regresión de (13) es una extensión de la anterior con otra dummy, esta vez para el año 1972, y un término de tendencia. La inclusión de las dummys se debe a la posible presencia de quiebre estructural en esos años, por reformas económicas o intervenciones políticas que pudieron generar cambios estructurales (Dorta, 2006). Finalmente, una versión de la función de producción agregada fue estimada incluyendo un polinomio de grado cuatro en la variable de tendencia temporal T, incorporación sugerida para capturar los desplazamientos de la función en el tiempo (Dorta, 2006). En la tabla están los resultados con que T3 y T4 resultaron ser significativos.
Los coeficientes β1 y β2 que se refieren a las elasticidades de producción con respecto al capital y al trabajo, respectivamente, son significativos individualmente en términos estadísticos al 1%. Sin embargo, en la segunda versión el estimado de la elasticidad producto-trabajo es negativo lo cual es contrario a la teoría y al signo esperado a priori. En la tercera regresión los coeficientes estimados asociados a las tendencias temporales son significativos, pero la suma de las elasticidades del producto respecto a los factores es mayor que uno, evidencia que es contraria a la hipótesis de rendimientos constantes a escala en la función CD. El ajuste que presenta mejor comportamiento es el primero, con una elasticidad producto-capital de 0,66, y producto-trabajo de 0,36.
De acuerdo a la literatura econométrica, los modelos estimados en los niveles de las variables pueden arrojar resultados espurios. No obstante, un modelo puede ser estimado con las series originales si las mismas tienen igual orden de integración, y los residuos de la estimación son integrados de orden cero o estacionarios (Engle y Granger, 1987). En efecto, se encontró cierta evidencia que sugiere que los residuos de las regresiones en niveles de la función de producción son estacionarios al 5% en la mayoría de las especificaciones de las pruebas ADF y PP sin constante y sin tendencia (SCST), y en otros casos con constante y con tendencia (CCCT), por tanto existe evidencia de cointegración en las tres regresiones de la ecuación (13).
Tabla III
Resultados función CD (ecuación 13)
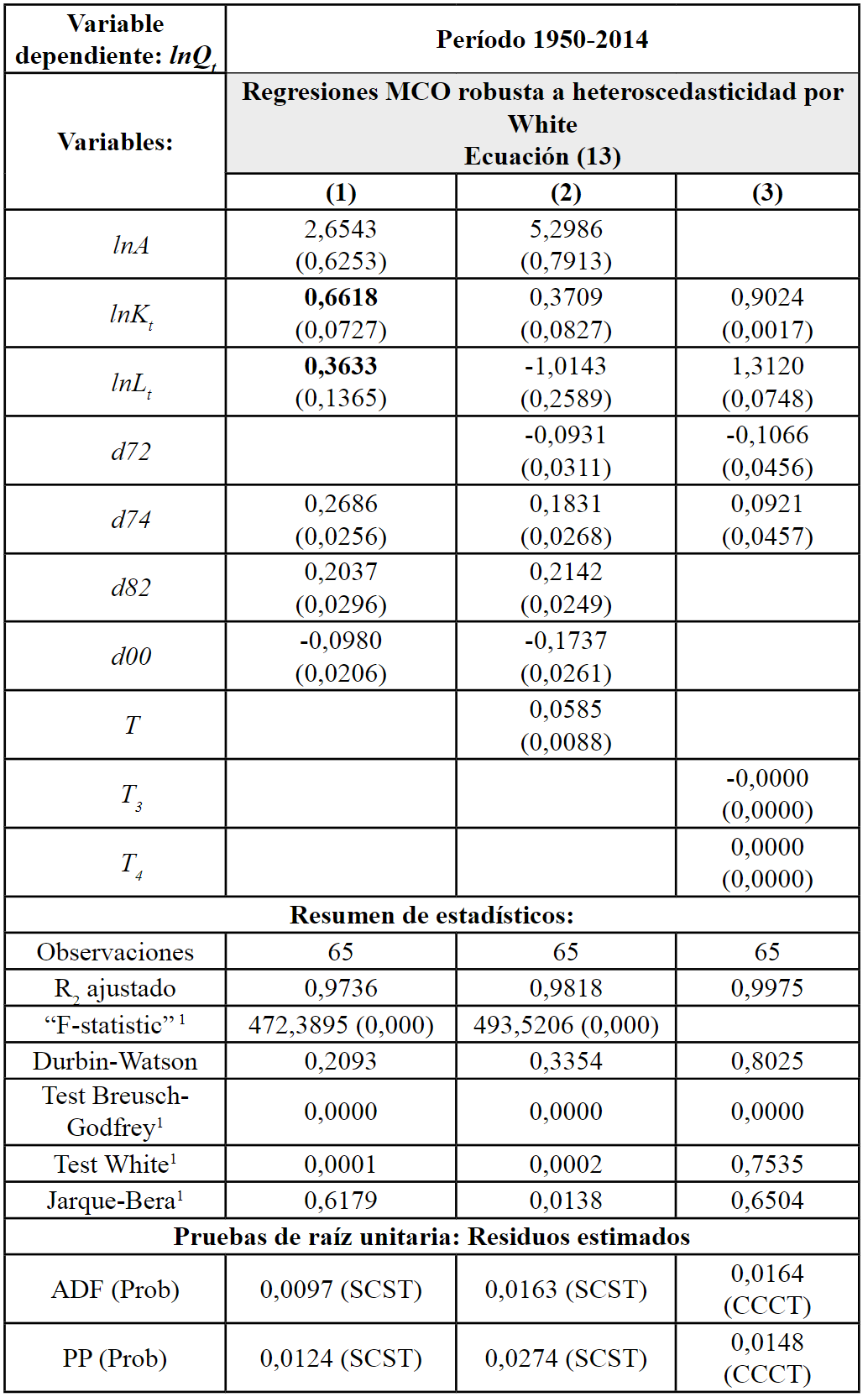
Fuente: Elaboración propia (2018), con base a resultados en Eviews 7.
1 Probabilidades del estadístico de prueba.
En consecuencia, las estimaciones descritas son consistentes, siendo la de mejor comportamiento la primera, donde la función de producción exhibe claramente rendimientos constantes a escala, y la participación del capital en el producto es de 0,66 y del trabajo en torno a 0,36. En otros términos, en la economía ecuatoriana durante el período analizado la evidencia estadística hallada con la función CD sugiere que, manteniendo constante el insumo capital, un incremento de 1% en el insumo trabajo provocó, en promedio, un incremento de cerca de 0,36% en la producción. En forma similar, manteniendo constante el insumo trabajo, un incremento de 1% en el insumo capital generó, en promedio, un incremento de cerca de 0,66% en la producción. Como la función CD parte de que hay rendimientos constantes a escala, entonces se comprueba la hipótesis β1 + β2 = 1, es decir si es válida la restricción de igualdad lineal indicada. Se aplicó el Test de Wald para contrastar la hipótesis nula β1 + β2 = 1, resultando el p-valor del estadístico F mayor a 0,05, en consecuencia no se puede rechazar la hipótesis nula de rendimientos constantes a escala.
Por último, la Tabla IV presenta tres estimaciones de un Modelo de Corrección del Error, derivado de cada una de las versiones del modelo (13). Así mismo, la tabla en referencia contiene dos estimaciones del modelo recogido en la ecuación (14). Como se puede ver, en las diferentes versiones del MCE el parámetro que mide la elasticidad del producto al capital es significativo, con el signo esperado a priori y en magnitud bastante cercano al de la primera regresión del modelo (13). En la regresión en tasas de crecimiento (ecuación 14) se mantienen los mismos resultados respecto al efecto del capital sobre el producto, no obstante en ambos casos disminuyó significativamente la magnitud de la elasticidad del producto al trabajo. En el caso de las versiones del MCE la de mejor comportamiento parece ser la primera con una bondad de ajuste de 0,46, sin problemas de autocorrelación y heteroscedasticidad, y con residuos distribuidos como una normal y estacionarios. Como se ve en la tabla, las hipótesis de cada supuesto probabilístico de los modelos son contrastadas mediante las pruebas estadísticas comúnmente usadas en la literatura (Prueba Breusch-Godfrey, Prueba White y Prueba Jarque-Bera de normalidad de los residuos) .
Tabla IV
Resultados Ecuación (13) en un MCE y ecuación (14)
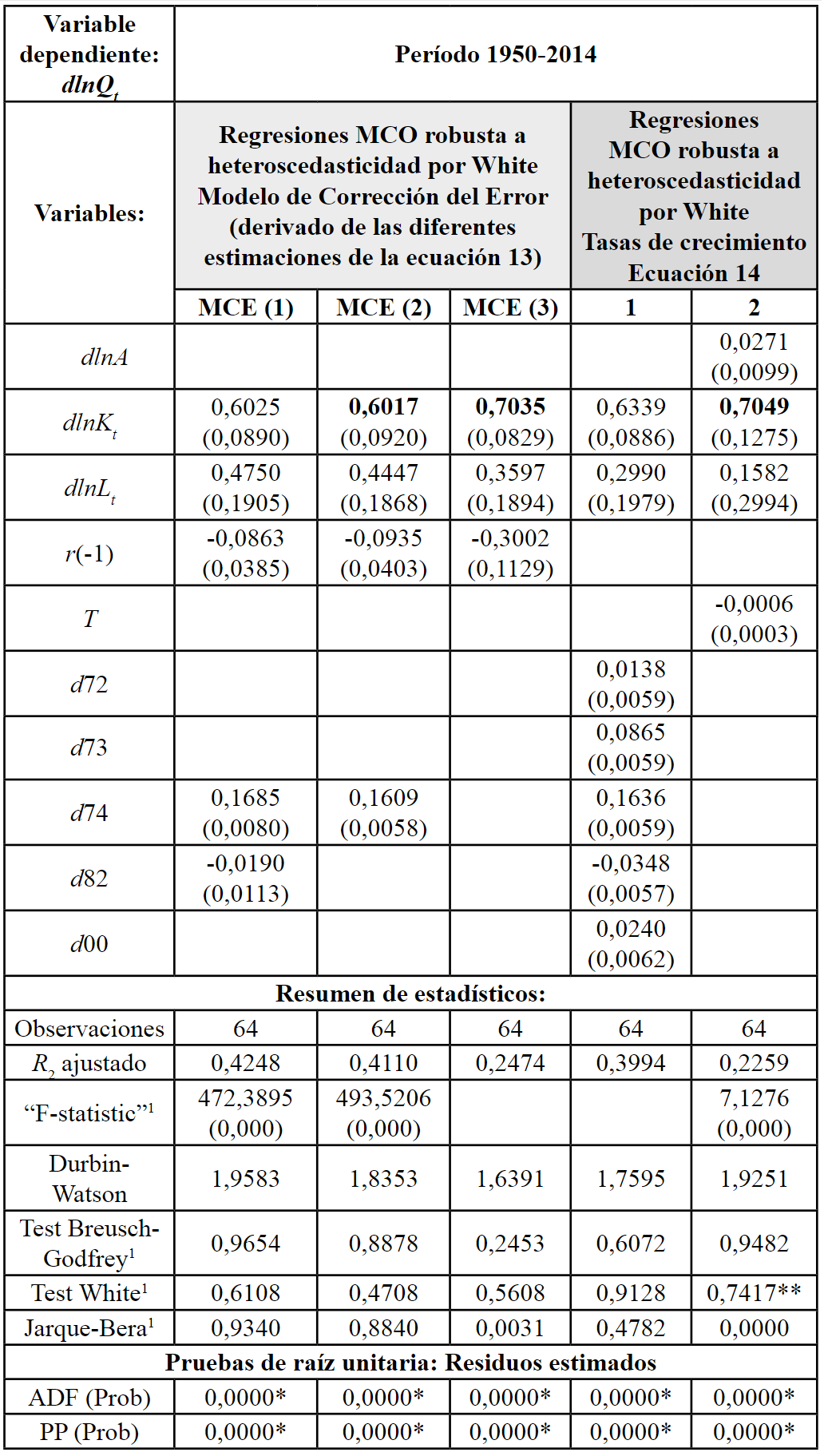
Fuente: Elaboración propia (2018), con base en Eviews 7.
* Residuos estacionarios en todas las especificaciones al 1%; ** La prueba es sin términos cruzados.
1 Probabilidades del estadístico de prueba.
El término r(-1) representa el error estimado del modelo de cointegración (todas las regresiones de la Tabla III pueden interpretarse como estimaciones de una ecuación de cointegración entre el producto y los insumos a largo plazo), que mide la velocidad de ajuste del desequilibrio a largo plazo. De acuerdo a la evidencia, el parámetro que acompaña al término de ajuste del desequilibrio es negativo, como se espera según la teoría de cointegración y corrección del error, y significativo al 5%.
Las variables dummy de 1974 y 1982 resultaron estadísticamente significativas, y con el signo esperado de acuerdo a los hechos estilizados de la economía ecuatoriana. En ese sentido, el Ecuador se vio beneficiado con el incremento de los precios del petróleo derivado del shock en los primeros años de los setenta, mientras que en 1982 comenzó a mostrar una desaceleración en su crecimiento en medio de la crisis de la deuda externa. En este modelo de corrección del error, la elasticidad producto-capital y la elasticidad producto-trabajo son, respectivamente, 0,60 y 0,48. De acuerdo al Test de Wald, no se puede rechazar la hipótesis de rendimientos constantes.
En el caso de las regresiones de la ecuación (14) de la función de producción en tasas de crecimiento, la primera regresión sin término constante parece mostrar mejor comportamiento en términos teóricos y empíricos. En esta versión, la elasticidad del producto al capital (trabajo) es de 0,63 (0,30), y de nuevo la evidencia estadística no permite rechazar la existencia de rendimientos constantes a escala en la función de producción.
En promedio, las mejores regresiones de la forma agregada de la función de producción CD indican una elasticidad del producto al capital y al trabajo en torno a 0,60-0,70 y 0,30-0,47 respectivamente, lo cual sugiere que la participación del capital en el producto del Ecuador ha sido bastante alta durante el período. Estos resultados son mayores a la estimación de la participación del capital en el producto reportado por Bernanke y Gürkaynak (2002), y cercanos a los de otras economías latinoamericanas según Elias (1992) y Aquino y Ramírez (2017).
Se ha expuesto que una alta participación del capital en el ingreso corresponde a una función de producción ampliada con capital humano (Sala-i-Martin, 2000: 48; Aquino y Ramírez, 2017), no obstante Samaniego (1995) presenta evidencia para el Ecuador de un aporte marginal bajo de la educación a partir de estudios universitarios y de postgrados al ingreso y salario de los individuos con estas calificaciones (1995:136,146-147).
En tal sentido, Hentshel (1994: 70) alega que el ambiente político influyó fuertemente en contra de la mano de obra y a favor de los bienes de capital. Como resultado de la inestabilidad política y la incertidumbre causada por cambios en el entorno macroeconómico, la asignación de recursos por medio del mercado pudo haber causado en el Ecuador un incremento en el precio del capital, pues los inversionistas esperan una mayor tasa de rentabilidad o premium conforme se deteriora el ambiente político y económico.
Al mismo tiempo, la alta participación del capital en el ingreso puede deberse a la alta proporción de empleo informal dentro del empleo total, que sesga la verdadera participación del trabajo, caso que se presenta a menudo entre las economías en desarrollo o con mercados de trabajo con rigideces donde imperan contratos entre patronos y trabajadores, y la remuneración no se rige por el principio de la productividad marginal .
Karabarbounis y Neiman (2013) plantean que la participación del trabajo dentro del ingreso ha declinado sustancialmente en los últimos 40 años debido al decrecimiento en el precio relativo de los bienes de inversión, lo cual ha inducido a las empresas a ajustar trabajo en beneficio del uso de capital. Maarek y Orgiazzi (2015) sostienen que conforme una economía pasa de ingreso bajo a ingreso medio, solo una parte de los trabajadores son ocupados en los sectores con altos niveles de productividad, donde la demanda de trabajo es baja y los salarios reflejan la baja productividad de las empresas de sectores tradicionales, por lo que la participación del trabajo decrece y sube la retribución del capital durante esta etapa.
Estimaciones de la forma intensiva:
La Tabla V presenta tres ajustes de la ecuación (15). Según la evidencia, el tercer ajuste (con un polinomio de tercer grado en la variable T) tiene la más alta bondad de ajuste, más el término constante que representa al parámetro de la tecnología es negativo, y la elasticidad del producto por trabajador es más que proporcional respecto al capital por trabajador. La primera versión tiene mejor comportamiento estadístico que la segunda, pues en esta última la variable de tiempo no es estadísticamente diferente de cero a ningún nivel de significación.
Tabla V
Resultados función CD intensiva (ecuación 15)
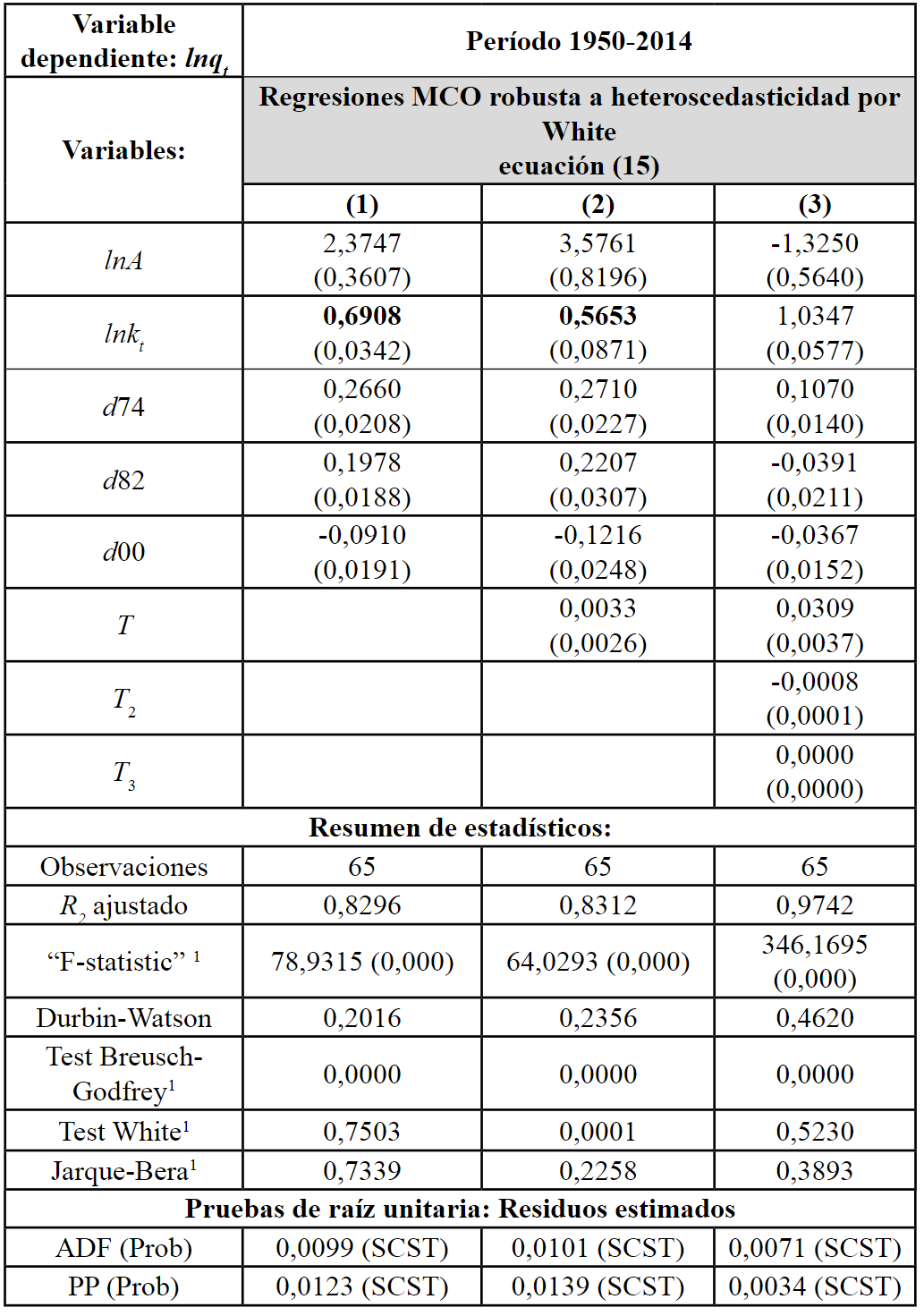
Fuente: Elaboración propia (2018), con base en Eviews 7. 1 Probabilidades del estadístico de prueba.
En el primer ajuste todas las variables son significativas al 1%, la elasticidad del producto por trabajador respecto al capital por trabajador es de 0,69. Por tanto, la elasticidad del producto al trabajo (1 –α) es cercana a 0,31. Por último, el R2 es alto y los residuos son estacionarios según ADF al 1% y PP al 5%, por lo que el modelo esta correctamente especificado e indica una posible cointegración a largo plazo.
En la Tabla VI se exponen los resultados del modelo de corrección del error derivado de cada una de las relaciones de cointegración mostradas en la tabla anterior. En todos los casos, el parámetro de ajuste del desequilibrio fue significativo y con el signo esperado, y las elasticidades del producto al capital van de 0,56 a 0,62 .
Finalmente, las dos últimas columnas de la tabla reportan los resultados de la ecuación (16). Se llevaron a cabo dos regresiones, una con constante y con tendencia y la otra sin término constante y sin la variable de tiempo. La elasticidad del producto por trabajador respecto al capital por trabajador, según nuestras estimaciones, se encuentra cerca de los valores hallados antes. En conjunto, los resultados de la función estimada en forma intensiva sugieren que una incremento del 1% en el stock de capital genera un incremento entre 0,56% y 0,69% en el producto por trabajador.
Esto representa una participación alta del ingreso del factor capital dentro del ingreso total generado en la economía ecuatoriana. En consecuencia, la evidencia hallada sugiere que en el Ecuador, durante el período estudiado, la participación del capital dentro del producto es superior a la participación del trabajo. Finalmente, cabe destacar que estos resultados son válidos dentro del contexto de los supuestos del modelo planteado.
Como último ejercicio empírico, y para complementar los resultados hallados, se efectuó la Prueba de Causalidad de Granger (Tabla VII). Los resultados hallados indican que la variable capital por trabajador k causa, en el sentido de Granger, a la variable producto por trabajador . En efecto, del cuadro se desprende que, dada la probabilidad del estadístico F de prueba, se rechaza la hipótesis nula de que k no causa en el sentido de Granger a y, es decir se acepta la hipótesis alternativa de que k si causa a y; no obstante, la hipótesis de que y no causa a k no se puede rechazar.
Tabla VI
Resultados Ecuación (15) en un MCE y ecuación (16)
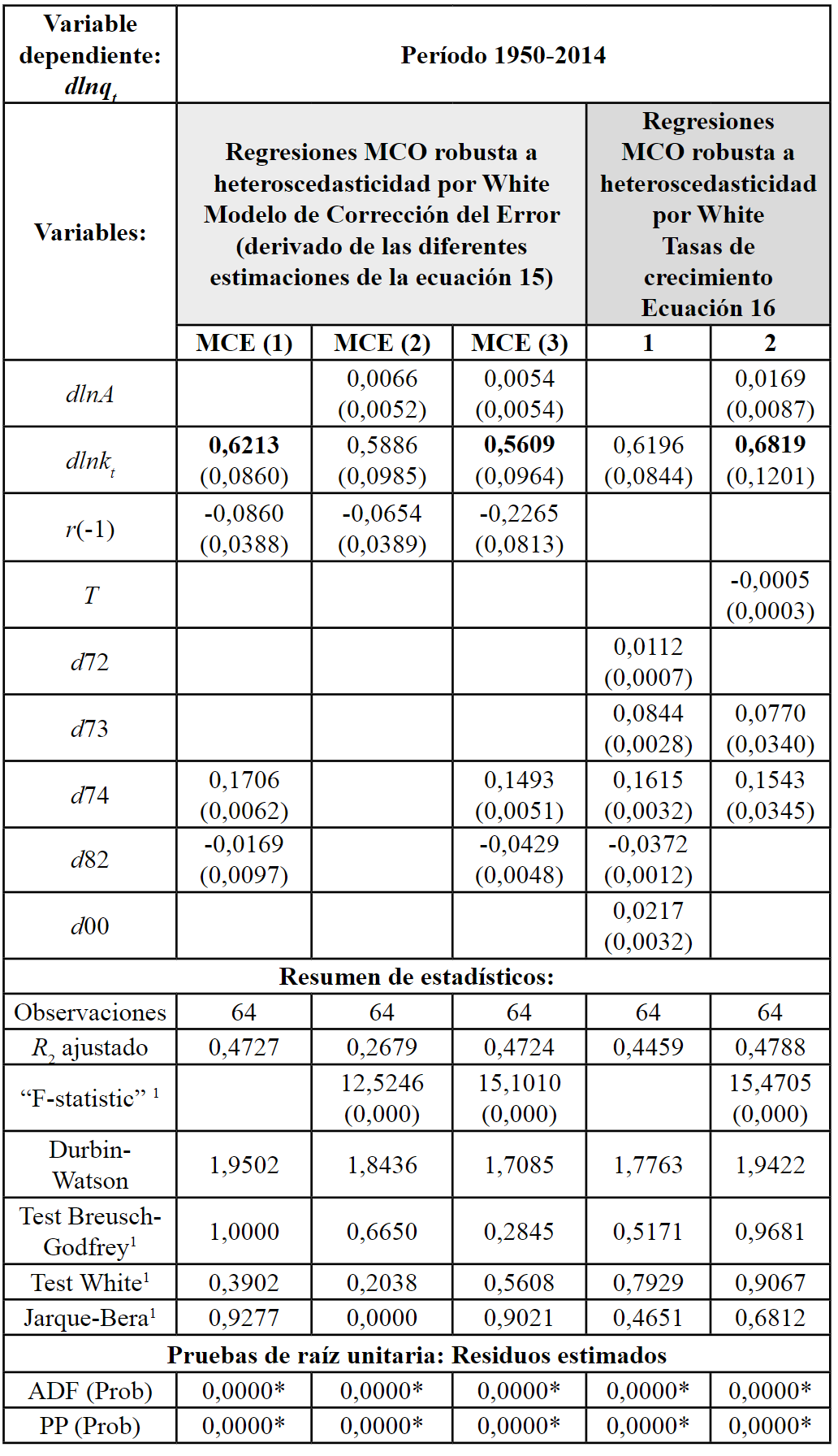
Fuente: Elaboración propia (2018), con base en Eviews 7.
* Residuos estacionarios en todas las especificaciones al 1%. 1 Probabilidades del estadístico de prueba.
Tabla VII

Prueba de Causalidad de Granger
Fuente: Elaboración propia (2018), con base en Eviews 7.
VI. CONCLUSIONES
El crecimiento económico del Ecuador ha sido significativo en los últimos años. El producto per cápita del Ecuador relativo a EE UU ha pasado de casi 0,11 en 1999 a 0,21 en 2014. Si bien aún no puede considerarse un éxito de crecimiento económico, el reciente repunte del crecimiento ecuatoriano invita a examinar sus posibles causas. Este trabajo ha brindado una de las condiciones necesarias para investigaciones futuras en esta área.
La metodología de Solow (1957) permite descomponer el crecimiento observado entre el crecimiento del capital, el crecimiento del trabajo, y el crecimiento de la productividad total. Este último componente se estima de forma residual si se disponen de medidas del crecimiento del producto y de los factores, junto a las participaciones de estos en el ingreso nacional. En este caso, las participaciones son iguales a la elasticidad del producto al capital y al trabajo, según el modelo de Solow, que utiliza una función CD. Usualmente, las estimaciones de la función CD son consistentes con las participaciones esperadas de cada factor, por lo que sigue siendo usada por la literatura para ello.
Acá se ha asumido esta alternativa, y en efecto se estimaron diferentes especificaciones econométricas de la función CD. Los resultados hallados muestran participaciones promedios del capital en torno a 0,60-0,70. Mientras que la participación del trabajo (elasticidad producto-trabajo) se encuentra en el rango de 0,31-0,47. Los valores aquí reportados para el Ecuador son próximos a la elasticidad del producto al capital de Colombia, México y Perú en Elias (1992), y para el Ecuador en Astorga y Valle (2003).
Las pruebas estadísticas confirman que los modelos están bien especificados y conservan las propiedades deseadas. El Test de Wald permitió comprobar la hipótesis de rendimientos constantes a escala en la función de producción, hallándose evidencia preliminar de que no es posible rechazar tal hipótesis para la economía del Ecuador.
Desde el punto de vista teórico, los resultados resaltan los patrones de inequidad en la distribución del ingreso generado en la producción, a favor del capital y en detrimento del factor trabajo. En tal sentido, probablemente como el Ecuador es una economía con una condición petrolera significativa, siendo ésta una actividad económica intensiva en capital, posiblemente haya un sesgo en la retribución percibida por este factor productivo, que sobreestima las participaciones factoriales.
A pesar de las limitaciones del análisis, dos reflexiones adicionales merecen ser expuestas. En primer lugar, investigaciones futuras deben ahondar en las razones por las que el capital físico parece tener una mayor participación en el producto en el Ecuador. Son necesarios ajustes del capital por su tasa de utilización y/o por algún indicador de calidad, en función de la disponibilidad de datos, y ajustes del trabajo para considerar la educación, como medida más amplia de capital humano, o el número de horas efectivamente trabajadas. En segundo lugar, las estimaciones presentadas brindan una base para el cálculo de la contabilidad del crecimiento, por lo que se invita a posteriores investigaciones aplicar dicho enfoque.
Otros trabajos ofrecen una baja participación del trabajo en el producto en los países en desarrollo, en comparación a los que reportan los países industrializados (ver,
e.g., Growiec
et al., 2018; Trapp, 2015; Bernanke y Gürkaynak, 2002; Gollin, 2002: 473; Elias, 1992). No obstante, Karabarbounis y Neiman (2013) muestran una declinación importante en los últimos años de la participación del trabajo en el ingreso en un amplio grupo de países industrializados.
La primera y la tercera regresión presentan la mejor bondad de ajuste, y los errores estimados conservan las propiedades clásicas (normalidad, homoscedasticidad y no autocorrelación), por lo que son regresiones consistentes.
La verificación de los supuestos estadísticos subyacentes a la especificación permite comprobar si el modelo elegido y el diseño del experimento se acercan al planteamiento teórico.
La demostración se encuentra en Chiang y Wainwrigth (2006: 385-386).
La demostración se encuentra en Chiang y Wainwrigth (2006: 385-386).
Es decir, f(
λx)=
λf(x).esta propiedad es conocida como homogeneidad de grado uno. Similarmente, la función de producción exhibe rendimientos crecientes (decrecientes) a escala si el producto aumenta en mayor (menor) proporción que todos los insumos.
Referencias
- Ackerberg, Daniel A.; Caves, Kevin; & FRAZER, Garth (2015). Identification properties of recent production function estimators. Econometrica, 83 (6). Pp. 2411–2451.
- Aiyar, Shekhar, & DALGAARD, Carl J. (2009). Accounting for productivity: Is it OK to assume that the world is Cobb–Douglas? Journal of Macroeconomics, Vol. 31. Pp. 290–303.
- Antràs, Pol (2004). Is the U.S. aggregate production function Cobb-Douglas? New estimates of the elasticity of substitution. Contributions to Macroeconomics, Vol. 4 (1).
- Aquino, Juan, & Ramírez, N.R. (2017). Estimating factor shares from nonstationary panel data. Peruvian Economic Association, Working Paper No. 89, February 2017.
- Aravena, Claudio (2010). Estimación del crecimiento potencial de América Latina. Serie Macroeconomía del desarrollo No. 106, CEPAL, Santiago de Chile, 2016. Pp. 1-26.
- Arrow, Kenneth J.; CHENERY, H. B.; MINHAS, B. S.; & SOLOW, Robert M. (1961). Capital labor substitution and economic efficiency. En: Review of Economics and Statistics, Vol. 43, No. 3, agosto 1961, USA. Pp. 225-250.
- Astorga, Alfredo, & VALLE, Angélica (2003). Estimación del PIB potencial para el caso del Ecuador. Cuestiones Económicas, Vol. 19, No. 2:3, Quito, Ecuador. Pp. 5-47.
- Azofeifa, Ana Georgina, & VILLANUEVA S., Marlene (1996). Estimación de una función de producción: caso Costa Rica. Banco Central de Costa Rica, Departamento de Investigaciones Económicas, División Economía, marzo de 1996.
- Barro, Robert J. (1998). Notes on growth accounting. NBER Working Paper No. 6654, Julio de 1998.
- Barro, Robert J., & SALA-I-MARTIN, Xavier (2004). Economic growth. The MIT Press, Massachusetts Institute of Technology, Cambridge, USA, Second edition.
- Bellod R., José F. (2011). La function de producción Cobb-Douglas y la economía española. Revista de Economía Crítica, No. 12, España. Pp. 9-38.
- Bernanke, Ben S., & Gürkaynak, Refet S. (2002).Is growth exogenous? Taking Mankiw, Romer, and Weil seriously. NBER Working Paper No. 8365, Julio de 2001.
- Chiang, Alpha C., & Wainwrigth, Kevin (2006). Métodos fundamentales de economía matemática. Editorial McGraw-Hill Interamericana, México, Cuarta edición.
- Cobb, Charles W., & Douglas, Paul H. (1928). A theory of production. American Economic Review, Vol. 18, USA. Pp. 139 – 165.
- Collard-Wexler, Allan, & De Loecker, Jan (2016). Production function estimation with measurement error in inputs. NBER Working Paper No. 22437, Julio de 2016.
- Dorta, Miguel (2006). La función de producción, el producto potencial y la inflación en Venezuela (1950-2005). Banco Central de Venezuela, Serie Documentos de Trabajo, No. 87, mayo de 2006.
- Duffy, J., & Papageorgiou, C. (2000). A cross-country empirical investigation of the aggregate production function specification. Journal of Economic Growth, 5. Pp. 87–120.
- Elias, Victor J. (1992). Sources of growth: A study of seven Latin American economies. ICS Press, San Francisco, 1992.
- Engle, R. F., & Granger, C. W. J. (1987). Cointegration and Error Correction: Representation, Estimation, and Testing. Econometrica, Vol. 55, USA. Pp. 251-276.
- Felipe, Jesus, & y ADAMS, Gerard F. (2005).The estimation of the Cobb-Douglas function: a retrospective view. Eastern Economic Journal, Vol. 31, No. 3.Pp. 427-445.
- Gollin, Douglas (2002). Getting income shares right. Journal of Political Economy, Vol. 110 (2). Pp. 458-474.
- Growiec, Jakub; Mcadam, Peter; & Muck, Jakub (2018). On the optimal labor income share. Szkoła Główna Handlowa Warszawie, Collegium of Economic Analysis Working Paper Series.
- Hentshel, Jesko (1994). Comercio y crecimiento en el Ecuador: una visión parcial de equilibrio. Cuestiones Económicas, No. 23, diciembre, Quito, Ecuador. Pp. 57-74.
- Intriligator, Michael D. (1971). Mathematical optimization and economic theory. Prentice-Hall, Englewood Cliffs, New Jersey, USA, First edition.
- Karabarbounis, Loukas, & NEIMAN, Brent (2013). The global decline of the labor share. NBER Working Paper No. 19136, Junio de 2013.
- Maarek, Paul, & ORGIAZZI, Elsa (2015). Development and the labor share. THEMA Working Paper No. 2015-09, Université de Cergy-Pontoise, France.
- Miller, Eric (2008). An assessment of CES and Cobb-Douglas production functions. Congressional Budget Office, USA, June 2008. [En línea] Disponible en www.cbo.gov.
- Monge B., Carlos (2012). Estimación de una función de producción para Costa Rica: 1978-2010. Banco Central de Costa Rica, Documento de Trabajo No. 19-2012, Departamento de Investigaciones Económicas, junio 2012. Pp. 1-32.
- Nicholson, Walter (1997). Teoría microeconómica: principios básicos y aplicaciones. Editorial McGraw-Hill, Madrid, España, Primera Edición en español, 599p.
- Ontaneda, David (2017). El impacto de la dolarización oficial en la profundización financiera en Ecuador. Cuestiones Económicas, Vol. 27, No. 1:2, Ecuador. Pp. 11-43.
- Romer, David (2012). Advanced Macroeconomics. Editorial Mc Graw-Hill, New York, USA, Fourth Edition, 716p.
- Sala-I-Martin, Xavier (2000). Apuntes de crecimiento económico. Editorial Antoni Bosch, Barcelona, España, Segunda edición, 250p.
- Solow, Robert M. (1957). Technical change and the aggregate production function. The Review of Economics and Statistics, Vol. 39 (3), USA. Pp. 312-320.
- Suárez, Fernando (2010). Estimación de una función de producción agregada: Argentina 1975-2006. Ensayos de Política Económica, Vol. 4, Argentina. Pp. 54-87. Pontificia Universidad Católica Argentina.
- Weil, David N. (2006). Crecimiento económico. Editorial Pearson Educación, S.A., Madrid, 616p.
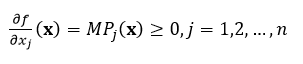 donde
donde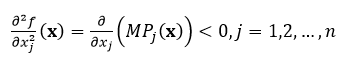 (Intriligator, 1971:180), que se conoce como la hipótesis de los retornos decrecientes: la agregación adicional de más y más de uno de los insumos, manteniendo fijos los restantes, genera disminuciones de la producción total.
(Intriligator, 1971:180), que se conoce como la hipótesis de los retornos decrecientes: la agregación adicional de más y más de uno de los insumos, manteniendo fijos los restantes, genera disminuciones de la producción total.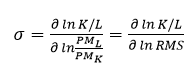 . Por tanto, en el caso de rendimientos constantes de escala, la elasticidad de sustitución de la función es igual a 1, y el parámetro de sustitución es igual a cero. La función de producción en la que σ =1 se denomina función de producción Cobb-Douglas (Nicholson, 1997: 214) y equivale a participaciones constantes de K y L.
. Por tanto, en el caso de rendimientos constantes de escala, la elasticidad de sustitución de la función es igual a 1, y el parámetro de sustitución es igual a cero. La función de producción en la que σ =1 se denomina función de producción Cobb-Douglas (Nicholson, 1997: 214) y equivale a participaciones constantes de K y L.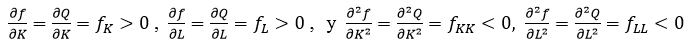 . El Modelo de Solow sigue el caso especial de cambio técnico neutro en el sentido de Hicks (Solow, 1957: 312), por lo que la función de producción toma la forma especial:
. El Modelo de Solow sigue el caso especial de cambio técnico neutro en el sentido de Hicks (Solow, 1957: 312), por lo que la función de producción toma la forma especial: 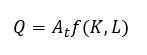 (2)
(2)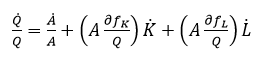 (3)
(3)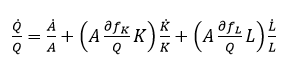 (4)
(4)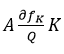 es la participación del capital en el ingreso nacional, mientras que
es la participación del capital en el ingreso nacional, mientras que 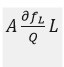 es la participación del trabajo.
es la participación del trabajo. 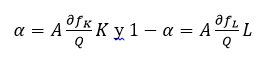 y entonces:
y entonces: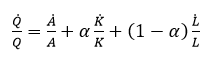 (5)
(5)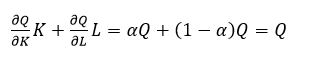 (7)
(7)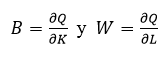 por tanto dada (7):
por tanto dada (7):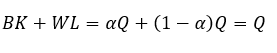 (8)
(8)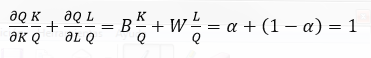 (9)
(9)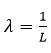 se obtiene la forma intensiva:
se obtiene la forma intensiva: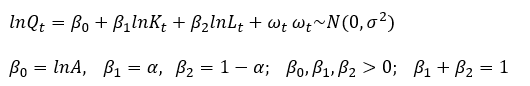 (13)
(13)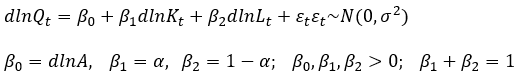 (14)
(14)





