https://doi.org/10.22267/rtend.212202.16

 

APLICACIÓN DEL MODELO DE AJUSTE PARCIAL NERLOVIANO PARA ESTIMAR LA ELASTICIDAD DE LA OFERTA DE PLÁTANO EN COLOMBIA

APPLICATION OF THE NERLOVIAN PARTIAL ADJUSTMENT MODEL TO ESTIMATE PLANTAIN SUPPLY ELASTICITY IN COLOMBIA

 

APLICAÇÃO DO MODELO DE AJUSTE PARCIAL NERLOVIANO PARA ESTIMAR A ELASTICIDADE DA OFERTA DO PLÁTANO NA COLÔMBIA

 

Por: Susan Cancino1, Giovanni Orlando Cancino Escalante2

 

1 Magíster en Administración de Negocios, Universidad de Nottingham, Reino Unido. Miembro del Grupo de Investigación Biotecnología Vegetal, Universidad de Pamplona. ORCiD: 0000-0001-7827-8502. E-mail: susancancino@hotmail.com, Colombia.

2 PhD en Biotecnología, Universidad de Nottingham, Reino Unido. Profesor Titular Universidad de Pamplona. Director del Grupo de Investigación Biotecnología Vegetal, Universidad de Pamplona. ORCiD: 0000-0002-3812-1129. E-mail: gcancino@unipamplona.edu.co, Colombia.

 

Recibido: 2 de febrero de 2021                         Aprobado: 21 de junio de 2021

 

 

Resumen

El objetivo del presente estudio fue estimar la respuesta de la oferta del plátano y las elasticidades de corto y largo plazo mediante el modelo de ajuste parcial desarrollado por Nerlove, tomando como base el periodo entre 2000 y 2018. Se aplicó un diseño de investigación explicativo, cuantitativo y correlacional y para la estimación empírica se empleó la metodología de los vectores autorregresivos. Los resultados indicaron que los coeficientes asociados al precio y producción rezagadas fueron positivos, significativos y coherentes con la teoría económica. Las elasticidades calculadas de corto plazo fueron inelásticas y similares a estudios relacionados con los cultivos permanentes por lo cual se puede inferir que las políticas de precios no son una herramienta eficaz para aumentar la oferta del plátano debido a la baja respuesta de la producción a movimientos en los precios.

Palabras Clave: cointegración; estacionariedad; expectativas de precios; respuesta oferta; vector autorregresivo.

JEL: C01; Q10; Q11; Q12; Q18

 

 

Abstract

The objective of this study was to estimate the response of the plantain supply and the short and long-term elasticities through the partial adjustment model developed by Nerlove, based on the period between 2000 and 2018. An explanatory, quantitative and correlational research design was applied and for the empirical estimation, the methodology of autoregressive vectors was used. The results indicated that the coefficients associated with lagged price and production were positive, significant and consistent with economic theory. The short-term elasticities were inelastic and similar to studies related to permanent crops, thus price polices are not an effective tool to increase supply due the low response to price movements.

Keywords: cointegration; stationarity; price expectations; supply response; vector autoregressive.
JEL: C01; Q10; Q11; Q12; Q18

 

 

Resumo

O objetivo deste estudo foi estimar a resposta da oferta do plátano e as elasticidades de curto e longo prazo por meio do modelo de ajuste parcial desenvolvido por Nerlove, para o período entre 2000 e 2018. Um desenho de pesquisa explicativo, quantitativo e de correlação, foi aplicada e para a estimativa empírica, utilizou-se uma metodologia vetorial auto-regresiva. Os resultados indicaram que os coeficientes associados ao preço e à produção defasados ​​foram positivos, significativos e consistentes com a teoria econômica. As elasticidades de curto prazo calculadas foram inelásticas e semelhantes a estudos relacionados com culturas permanentes, pelo que se pode inferir que as políticas de preços não são um instrumento eficaz para aumentar a oferta do plátano devido à baixa resposta da produção aos movimentos nos preços.

Palavras-Chave: cointegração; estacionariedade; expectativa dos preços, resposta oferta, vetor auto-regresivo
JEL: C01; Q10; Q11; Q12; Q18

 

Introducción

El plátano (Musa paradisíaca) es originario del sudeste asiático donde su cultivo a lo largo del tiempo se expandió hacia los demás continentes, concentrándose fundamentalmente en África, América Latina y el Caribe (Sánchez-Zúñiga et al., 2020; Espinal et al., 2005). La producción se concentra en su mayoría en los países africanos donde Uganda es el principal productor a nivel mundial con el 23,6% seguido de Camerún (23,2%) y Ghana (9,7%) (Organización de las Naciones Unidas para la Alimentación y la Agricultura [FAO], 2020). En efecto, es un producto tropical de gran importancia desde el punto de vista económico, puesto que su producción es un generador de ingresos y empleo en el sector rural. Asimismo, es un cultivo estratégico una vez que contribuye a la seguridad alimentaria de los países debido a sus propiedades nutricionales (Álvarez et al., 2020).

En Colombia, la producción agronómica del plátano en 2019 fue de 4.805.629 toneladas (ton), con un área sembrada de 536.443 hectáreas (ha) y un rendimiento promedio de 10,7 ha/tones concentrados en 786 municipios, donde el departamento de Arauca es el principal productor (17,4%) seguido de Meta (11,4%) y Antioquia (10,1%) (Ministerio de Agricultura y Desarrollo Rural, 2020).

De igual forma el cultivo ha sido una actividad con gran impacto en la economía del país por lo cual 213.950 familias se han dedicado a su producción, con un promedio de 3,5 ha por productor, generando 96.000 empleos directos e indirectos. Además, por sus características alimenticias hace parte de la canasta básica de las familias y gran parte de su producción es destinada al consumo interno. Sin embargo, los precios del plátano han sido afectados por la sobreoferta como consecuencia del aumento del área sembrada en los últimos cuatro años, afectando los ingresos y la rentabilidad económica de los productores (Ministerio de Agricultura y Desarrollo Rural, 2020).

En este sentido, y dada la gran importancia del sector agrícola en el desarrollo económico de los países, se han realizado diversos estudios y empleado distintos métodos para el análisis del comportamiento de los productores y la estimación de las elasticidades de la oferta de productos agrícolas. En efecto, entre los métodos más utilizados se encuentra el de Nerlove, el cual introduce elementos dinámicos en la modelización de la función de oferta (Mekbib et al., 2014).

Es así que, dada la importancia social y económica que tiene el cultivo del plátano en Colombia, el entendimiento del comportamiento de sus precios se hace importante para la toma de decisiones de los agricultores como del gobierno y de los gremios, los cuales necesitan contar con herramientas eficientes para definir las políticas dirigidas al sector. De hecho, las políticas de precios han sido la base de las decisiones agrícolas en muchos países y cualquier incentivo o planificación de la producción requerirá de un conocimiento detallado de los factores que afectan la oferta (Briceño et al., 2005; Tripathi y Prasad, 2009; Huq y Arshad, 2010). Por lo tanto, el propósito del estudio fue estimar la respuesta de la oferta nacional del plátano frente a los cambios en su propio precio y a partir del resultado cuantificar las elasticidades precio de la oferta de corto y largo plazo. Para ello, el presente estudio desarrolló una aproximación conceptual al modelo de ajuste parcial, o de existencias elaborado por Nerlove (1958) y para la estimación empírica se empleó la metodología de los Vectores Autorregresivos (VAR).

El presente documento consta de 5 secciones, siendo la primera esta introducción. En la segunda se presentan los referentes teóricos y la tercera la metodología, los datos y variables empleados, la especificación y las pruebas efectuadas para el modelo propuesto. En las dos últimas secciones, se presentan los resultados y se exponen las conclusiones del estudio realizado.

 

Referentes teóricos

El modelo de Nerlove es de gran importancia en cuanto al establecimiento de un fundamento teórico para el análisis de la oferta de productos agrícolas. Se soporta en la idea de que los agricultores revisan su producción en cada periodo con base en los precios futuros o esperados y con referencia a los precios observados en el pasado. El método comprende inicialmente la estimación de una función de oferta la cual tiene la siguiente forma (ecuación 1) (Askari y Cummings, 1977; Kohli, 1996; van Wyk y Treurnicht, 2012):

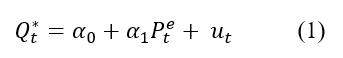
Donde  se refiere a la producción deseada en el periodo corriente;  el precio esperado en el tiempo t ; se refiere a la constante de la ecuación y  el coeficiente de ajuste que refleja la respuesta de la producción.

El modelo supone un mecanismo de ajuste parcial en el tiempo en el cual los agricultores revisan en cada periodo sus decisiones para lograr un nivel deseado de producción, por lo tanto, la producción en un periodo dado depende de la diferencia entre la producción deseada y la observada en periodos anteriores y se resume en la ecuación 2:

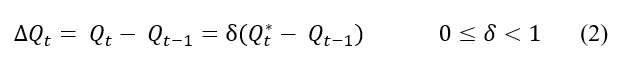
Donde:
 = producción observada en el periodo actual
 = producción observada en el periodo anterior
= producción deseada en el periodo t
δ = coeficiente de ajuste parcial

Igualmente, Nerlove incorpora en el modelo las expectativas de precios por lo cual afirma que los productores revisarán y corregirán los precios de los productos agrícolas de acuerdo con el error que cometieron al estimarlos en el periodo anterior expresado por la ecuación 3:

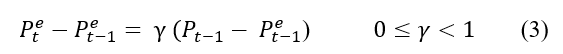
Donde  y  son los precios esperados en periodo t y t-1; el coeficiente de respuesta de las expectativas a los precios observados y el precio actual en el periodo t-1.
De esta forma, utilizando las tres ecuaciones y tomando las variables  y  y simplificándolas se obtiene , el cual muestra la producción en el periodo actual como una función lineal del precio y de la producción en el periodo anterior y un término de error (Ecuación 4):

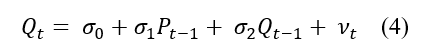
Según Quintero y López (2011) y Khan et al. (2019) el coeficiente  corresponde a la elasticidad en el corto plazo para el precio en el periodo anterior, mientras que la elasticidad en el largo plazo definida en un sistema de logaritmos estaría dada por la ecuación 5:

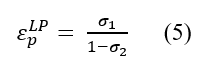
Es de esta manera como Khan et al. (2019) basado en lo expuesto por Nerlove realizaron un estudio en Khyber Pakhtunkhwa, Pakistán, para el periodo comprendido entre 1976 y 2010, cuya finalidad fue estimar la respuesta de la oferta de arroz ante variaciones en su propio precio y las elasticidades de corto y largo plazo. Para ello, utilizaron un modelo de vectores autorregresivos, encontrando que el precio rezagado del arroz posee un efecto positivo y significativo en la producción y que las elasticidades de precio de la oferta tanto en el corto (0,091) como en el largo plazo (0,037) fueron inelásticas.

A su vez, Dlamini (2018), mediante un modelo nerloviano adaptado, estimó la capacidad de respuesta de los productores de Suazilandia, África, con respecto a cambios en el precio de la papa y otros factores, así como, la elasticidad precio de la oferta. El autor concluyó que para el corto plazo el precio fue el factor de mayor influencia en la decisión de producción de los agricultores y que los factores diferentes al precio no fueron estadísticamente significativos.

De igual manera, Huq y Arshad (2010) estudiaron los efectos del cambio de los precios en la oferta de papa en Bangladesh para el periodo 1982-2006. Los autores fundamentaron el estudio en el modelo nerloviano, sin embargo, para la estimación empírica de las elasticidades emplearon la metodología de cointegración y de corrección de errores. Los resultados de la elasticidad en el corto y largo plazo fueron de 0,45 y 0,62, respectivamente, por lo cual se demostró que la oferta de papa es poco sensible a cambios en los precios. Mesike et al. (2010), por su parte, obtuvieron resultados similares al analizar la sensibilidad de la producción ante variaciones en los precios del caucho en Nigeria. En las elasticidades estimadas las mismas exhibieron inelasticidades con respecto a su propio precio en el corto (0,37) y largo plazo (0,20).

Igualmente, en los estudios de Mose et al. (2007) sobre la respuesta de la oferta de maíz con respecto a variaciones en el precio del fertilizante y su propio precio en el distrito de Trans-Nzoia, Kenya, los autores encontraron que los agricultores responden fuertemente a cambios en el precio del fertilizante cuya elasticidad en el corto plazo fue de -1,05, sin embargo, con relación a su propio precio éstos fueron inelásticos en el corto y largo plazo.

Para el caso colombiano, entre los estudios basados en los trabajos de Nerlove se destaca el de Quintero y López (2011) cuyo objetivo fue analizar la respuesta de la oferta de arroz paddy verde en Colombia para el periodo 1992-2009, mediante el análisis de cointegración y el modelo de vector de corrección de errores. Los resultados demostraron que la oferta de arroz paddy verde fue elástica, tanto en el corto como en largo plazo, respecto al área cultivada, e inelástica respecto a su propio precio y los costos de producción. Asimismo, Chique et al. (2006) utilizando la misma metodología de análisis estimaron la ecuación de oferta del arroz blanco para Colombia, por el cual también concluyeron que la oferta estimada fue elástica con respecto al precio y al área cosechada e inelástica con respecto a los precios de los factores e insumos.

Por último, Ramírez et al. (2004) utilizaron el modelo de Nerlove para estimar la respuesta de la producción de cultivos transitorios y permanentes en Colombia, entre ellos el arroz, trigo, papa, plátano y banano aplicando la metodología de mínimos cuadrados ordinarios. De los resultados obtenidos determinaron que la producción responde significativamente a variaciones en los precios y que las elasticidades en el corto plazo son inferiores en relación con las obtenidas en el largo plazo.

Metodología


De acuerdo con el propósito del estudio se aplicó un diseño de investigación explicativo, cuantitativo y correlacional. Las principales fuentes secundarias para la obtención de los datos fueron la Organización de las Naciones Unidas para la Agricultura y la Alimentación (FAOSTAT), la base de datos del Ministerio de Agricultura y Desarrollo Rural de Colombia (Agronet) y el Banco de la República, así como, informes y artículos económicos.

Datos y variables empleadas
La información utilizada para la elaboración del modelo econométrico corresponde a una serie de tiempo con periodicidad anual desde 2000 al 2018, siendo las variables utilizadas la producción (ton) y el precio por tonelada recibido por los productores de plátano en pesos colombianos (COP/ton). La serie de precios fue deflactada haciendo uso del índice de precios al productor (IPP; 2018 = 100) con el fin de eliminar los efectos de la inflación. Éstas se presentaron transformadas en logaritmos para una mejor interpretación económica y los datos se analizaron utilizando el paquete E-views®11.

Especificación del Modelo
El fundamento teórico del estudio se basó en el modelo de Nerlove (1958) y para la estimación empírica, se empleó la metodología de los vectores autorregresivos (VAR) con la finalidad de superar los problemas de regresiones espurias, resultados incoherentes y distorsionados asociados a técnicas de análisis econométricos tradicionales (Guzmán y García, 2008).

En el modelo VAR desarrollado por Sims (1980), todas las variables son consideradas endógenas por lo cual son explicadas por sus propios rezagos y por los rezagos ​​de las demás variables en un sistema de orden finito. En términos formales el VAR se define como (Ecuación 6) (Lutkepohl, 2005; Guzmán y García, 2008):

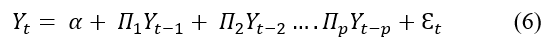
Donde  representa un vector de k constantes de orden k x 1;  un vector k x 1 de series de tiempo que se regresan;  se refiere a la matriz de coeficientes (k x k) y  corresponde a un vector kx1 que sigue un comportamiento de ruido blanco.

Por lo tanto, el estudio consideró las variables cantidad y precio del plátano rezagados cómo endógenas debido a que sus valores están determinados por la interacción simultánea de las relaciones del modelo. Asimismo, se asume que los productores de plátano en cada periodo revisan los precios de acuerdo al error que cometieron al estimarlo en el periodo anterior, así que, de acuerdo a Nerlove y Bassler (2001) la representación simplificada del precio esperado está dada como una función de los precios pasados. De la misma forma, el modelo incorporó el valor rezagado de la producción del plátano con la finalidad de representar el tiempo involucrado entre las decisiones de siembra y de cosecha, por los cuales se asume que las intenciones actuales de producción se verán reflejadas en las decisiones pasadas representada así, por la siguiente ecuación (7):

Donde  es el logaritmo de la producción de plátano;, son el logaritmo de la producción y del precio al productor del plátano rezagado un periodo;  se refieren a los coeficientes de corto plazo y  al termino del error.

Pruebas de estacionariedad y de cointegración
En un modelo VAR se requiere que las variables involucradas sean estacionarias, es decir, que sus medias, varianzas y covarianzas se mantengan constantes en el tiempo (Hamilton, 1994), por lo tanto, se utilizó la prueba de Dickey-Fuller aumentada (1979) (ADF) para determinar la existencia o no de raíces unitarias en las series temporales. La prueba asume como hipótesis nula la existencia de una raíz unitaria y cuanto más negativo es el valor obtenido, mayor la probabilidad de rechazo.

Igualmente, se aplicó la prueba de Johansen (1988) y Johansen y Joelius (1990) para identificar la existencia de cointegración entre las series de tiempo la cual se encuentra conformada por dos test: la traza donde se contrasta la hipótesis nula de no cointegración (HO: r = 0) contra la hipótesis alternativa de cointegración (H1: r > 0) y el máximo eigenvalue donde se contrasta la hipótesis nula de que el rango de cointegración es igual a r = 0 en contra de la alternativa de que el rango de cointegración es igual a r +1.
Selección del número de rezagos, pruebas de validez y test de causalidad de Granger
La selección del número de rezagos óptimos del modelo VAR se realizó de acuerdo con los criterios de información de Akaike (1974) y Schwarz (1978) y para el proceso de validación se emplearon las pruebas de normalidad de Jarque-Bera, heteroscedasticidad con términos no cruzados de White, autocorrelación mediante el test de Cholesky y cambios estructurales por medio de las pruebas CUSUM y CUSUM cuadrado. Además, se aplicó el test de Granger (1969) para establecer la relación de causalidad entre las variables.

 

Resultados

Evolución de los precios y cantidades del plátano
El plátano es un producto de permanente producción, sin embargo, sus cosechas se ven afectadas por épocas de fuerte invierno y verano, originando movimientos de alzas y/o bajas en la producción y el precio de acuerdo a los volúmenes ofrecidos y demandados. Es así como, en la Figura 1 se observa la evolución de los precios y las cantidades del plátano en Colombia durante el periodo 2015-2019.

Figura 1
Evolución de los precios y cantidades del plátano (2015-2019)

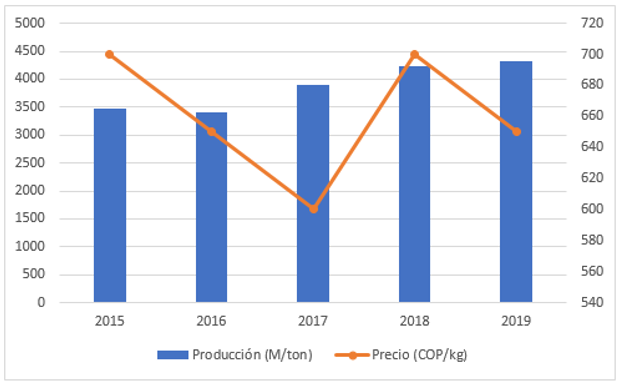
Fuente: elaboración propia con datos del Ministerio de Agricultura y Desarrollo Rural (2020).

Estimación del modelo empírico
El proceso planteado para estimar la respuesta de la oferta de plátano, y por su parte las elasticidades de corto y largo plazo, se inicia con la identificación de la presencia/ausencia de raíz unitaria en las series de tiempo por medio de la prueba ADF. En la Tabla 1 se muestran los resultados para las variables en logaritmos por lo cual se observa la existencia de raíz unitaria en nivel tanto con constante y tendencia y solo constante para los diferentes valores de significancia analizados. Sin embargo, al realizar la prueba en primeras diferencias no es posible aceptar la existencia de raíz unitaria para los niveles de significancia del 5% y 10% una vez que todos los valores del estadístico de pruebas en términos absolutos se encuentran por encima de sus valores críticos. De esta forma, se rechaza la hipótesis nula de presencia de raíz unitaria y se concluye que las series son estacionarias e integradas de orden 1.

Tabla 1
Valores estadísticos y críticos para las pruebas ADF

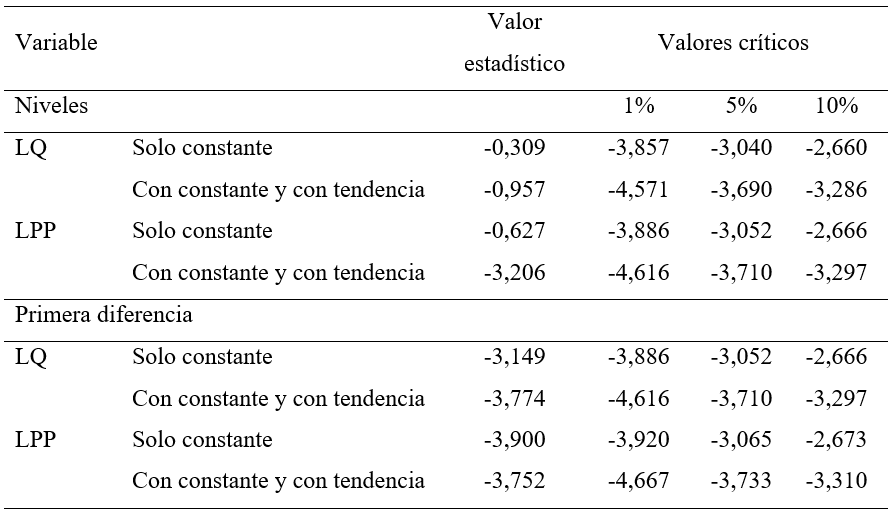
Fuente: elaboración propia.

De igual forma, se determinó la posible existencia de relaciones de largo plazo a través de la prueba de cointegración de Johansen, por lo cual los resultados se ven reflejados en la Tabla 2. Se evidencia que el valor estadístico de las pruebas traza y del máximo eigen-value aceptan la hipótesis nula al nivel del 5% a favor de una relación de no cointegración. Por consiguiente, se procedió a identificar la longitud de retraso mediante el criterio de información de Akaike y Schwarz obteniendo un número de rezagos igual a 1, lo cual se utilizó para estimar el modelo VAR propuesto.

Tabla 2
Prueba Johansen de cointegración

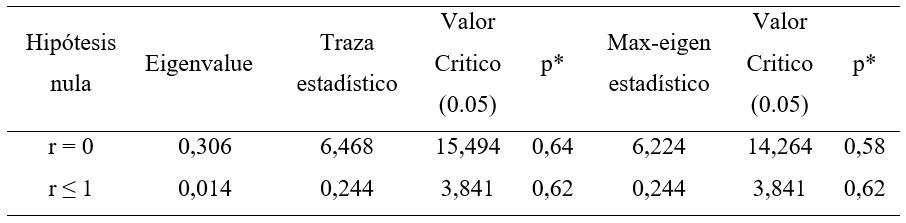
* Probabilidad MacKinnon (1996)
Fuente: elaboración propia.

De acuerdo con los resultados exhibidos en la Tabla 3, los coeficientes de regresión de las variables precio y producción rezagados del modelo VAR propuesto para el periodo analizado fueron estadísticamente significativos (p < 0,05) y presentaron la magnitud y los signos esperados; menores de uno y positivos. Además, el coeficiente de determinación (R2) demostró la amplia explicación del modelo por las variables utilizadas, que en su conjunto explicaron el 84% de los niveles de producción del plátano.

Tabla 3
Resultados VAR

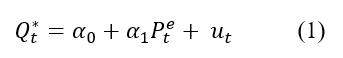
Fuente: elaboración propia.


Por otra parte, cabe señalar que los coeficientes obtenidos representan las estimaciones de las elasticidades de corto plazo de la oferta del plátano con respecto a su precio y producción. En este sentido, estos son inelásticos, es decir un incremento del 1% en el precio del plátano lleva a un incremento de la oferta en 0,112%; del mismo modo, un aumento del 1% en la producción aumenta la oferta del plátano en 0,829%.

Además, sobre la base de los resultados de los coeficientes se calcularon las elasticidades de la oferta de largo plazo tomando como referencia la ecuación 5, el cual revela que con relación a los precios ésta es igualmente inelástica (0,65), mientras que, para la producción es significativamente distinta a cero, positiva y elástica (4,84). Asimismo, se puede inferir que, si bien la elasticidad del precio es baja, la oferta en el corto plazo es relativamente más rígida cuando comparada con el largo plazo.

Por lo tanto, del análisis anterior se deduce que los resultados son congruentes con la teoría microeconómica y de los hechos empíricos propios de los cultivos permanentes. Es decir, la poca sensibilidad de la oferta del plátano a variaciones en los precios se debe posiblemente a la necesidad de inversión en adecuación de la tierra y en nuevas plantaciones por lo cual no se alcanza en el corto plazo, por consiguiente, un incremento en la producción requerirá de una ampliación de la capacidad productiva. Por lo tanto, si bien los coeficientes son positivos y estadísticamente significativos se puede inferir que los precios no parecen ser una herramienta eficaz en el incremento de la oferta del plátano.

En general, las estimaciones del presente estudio son similares a los resultados de los cultivos permanentes. Las elasticidades calculadas por otros investigadores son igualmente de respuesta baja como las obtenidas por Khan et al. (2019) y Quintero y López (2011) en arroz; Espinosa y Vaca (2011) en caña de azúcar y Mesike et al. (2010) en caucho, por los cuales todos presentaron elasticidades-precio de oferta de corto plazo entre 0,11 y 0,37.

Por otra parte, con el fin de comprobar el sustento estadístico del modelo se efectuaron pruebas de validez de los residuos, las cuales arrojaron resultados satisfactorios (Tabla 4). Es decir, no se evidenciaron problemas de normalidad, heteroscedasticidad y autocorrelación puesto que en todas las pruebas realizadas no se rechazaron las hipótesis nulas a un nivel de significancia del 5%, dado que el valor de la probabilidad fue mayor a 0,05.

Tabla 4
Resultados pruebas de diagnóstico

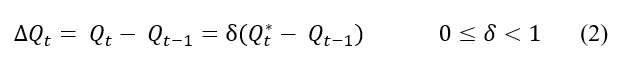
Fuente: elaboración propia.

Igualmente, se realizó la prueba de causalidad de Granger cuya finalidad fue establecer la existencia de una relación causal entre las series de tiempo. Como se observa en la Tabla 5, el precio y la producción del plátano presentaron probabilidades menores al 5% lo cual conlleva al rechazo de la hipótesis nula, y, por lo tanto, a la aceptación de que ambas variables se causan mutuamente en el sentido de Granger.

Tabla 5
Prueba de causalidad de Granger

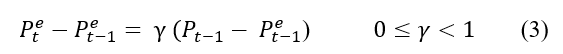
Fuente: elaboración propia.

Por último, se evaluó la condición de estabilidad mediante las pruebas CUSUM y CUSUM cuadrado, y a la simple vista (Figura 2), se observa que ninguno de los residuos sobrepasa las líneas criticas del 5% lo cual se concluye que no hay evidencia de un cambio estructural en el modelo propuesto.

 Figura 2
Pruebas CUSUM y CUSUM cuadrado

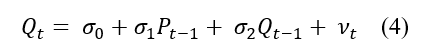
Fuente: elaboración propia.

Conclusiones

En el presente estudio se estimó la respuesta de la oferta de plátano y las elasticidades de corto y largo plazo. Para tal efecto, se empeló como soporte teórico el modelo nerloviano de ajuste parcial apoyado en la metodología de los vectores autorregresivos.

En particular, los resultados relacionados con la respuesta de la oferta del plátano señalan que los coeficientes asociados al precio y producción rezagados fueron positivos, estadísticamente significativos y coherentes con los sugeridos por la teoría microeconómica. Asimismo, se encontró que las elasticidades de corto y largo plazo fueron insensibles a variaciones en los precios, alcanzando valores inferiores a la unidad, lo cual permitió concluir que son inelásticas. En este sentido, se puede afirmar que los resultados obtenidos en la presente investigación son similares a estudios relacionados con otros cultivos permanentes por los cuales presentaron igualmente elasticidades-precio de oferta bajos. Cabe señalar que la prueba de máxima verosimilitud de Johansen indicó la no existencia de cointegración y se destaca que el modelo VAR estimado no posee problemas de normalidad, autocorrelación o heteroscedasticidad.

Por lo tanto, entender el comportamiento de los precios y su relación con la oferta es de gran importancia una vez que ayuda a los agricultores en la planeación y toma de decisiones y al gobierno y los gremios a plantear políticas efectivas para el sector. Es importante resaltar que, para el caso del presente estudio se observó que las políticas de precios parecen no ser una herramienta muy eficaz para aumentar la oferta de plátano debido a la baja respuesta de la producción a movimientos en los precios.

Por consiguiente, se concluye que las políticas diseñadas para fortalecer el sector deben estar orientadas a mejorar la eficiencia y rentabilidad de las unidades productivas por medio de un acompañamiento a los productores para la adopción de tecnologías y productos tecnológicos; facilitar el acceso a créditos para financiar los procesos productivos; fomentar la asociatividad; mejorar las habilidades de los productores para gestionar apropiadamente sus labores e impulsar la agricultura por contrato.

Finalmente, es evidente que el modelo propuesto es susceptible de mejora, por lo cual, se recomienda para estudios posteriores la realización de un análisis que incluya otras variables, como, por ejemplo, el precio del fertilizante, el área cosechada y precipitación, al igual que series de frecuencia más largas de tal forma que se obtenga una visión más amplia de los factores que afectan la respuesta de la oferta del plátano.

 

 

Referencias


(1) Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6), 716-723. https://doi.org/10.1109/TAC.1974.1100705

(2) Álvarez, L., León, A., Sánchez, M., & Cusme, B. (2020). Evaluación socioeconómica de la producción de plátano en la zona norte de la Provincia de los Ríos. Journal of Business and Entrepreneurial, 4(2), 86-97. https://doi.org/10.37956/jbes.v4i2.78

(3) Askari, H., & Cummings, J. (1977). Estimating agricultural supply response with the Nerlove model: A survey. Economic Review, 18(2), 257-292. https://doi.org/10.2307/2525749

(4) Briceño, F., Rojas, A., & Coydán, I. (2005). Politicas de precios en Chile: El caso de los cereales. Panorama Socioeconómico, 23(31), 58-70.

(5) Chique, V., Rosales R. & Samacá H. (2006). Efectos de la liberalización comercial: un análisis de equilibrio parcial para el sector de arroz en Colombia. Documento CEDE 2006-37.

(6) Dlamini, D. (2018). Supply response of potato to price and non-price factors in Swaziland. Archives of Business Research, 6(10), 78-85. https://doi.org/10.14738/abr.610.5248

(7) Espinal, C., Martínez, J., & Peña, M. (2005). La cadena de plátano en Colombia: Una mirada global de su estrucutra y dinámica 1991-2005. Bogotá: Observatorio Agrocadenas, Documento de trabajo No 61.

(8) Espinosa, A., & Vaca, P. (2011). Impactos y consecuencias en el sector azucarero en Colombia a partir del TLC con la Unión Europea. Horizontes Empresariales, 11(2), 7-34.

(9) Organización de las Naciones Unidas para la Alimentación y la Agricultura [FAO]. (2020). Datos estadísticos. http://www.fao.org/faostat/es/#data/QC

(10) Dickey W. & Fuller, D. (1979). Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association, 74(366), 427-431. https://doi.org/10.2307/2286348

(11) Granger, C. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 37(3), 424-438. https://doi.org/10.2307/1912791

(12) Guzmán, M., & García, A. (2008). El modelo VAR y sus principales problemas. Panorama Económico, 3(6), 95-117.

(13) Hamilton, J. (1994). Time Series Analysis. Princeton University Press.

(14) Huq, A., & Arshad, M. (2010). Supply response of potato in Bangladesh: A vector error correction approach. Journal of Applied Sciences, 10(11), 859-902. https://doi.org/10.3923/jas.2010.895.902

(15) Johansen, S. (1988). Satistical analysis of cointegrating vectors. Journal of Economic Dynamics, 12(2), 231-254. https://doi.org/10.1016/0165-1889(88)90041-3

(16) Johansen, S., & Juselius, K. (1990). Maximum likelihood estimation and inference on cointegration with applications to the demand for money. Oxford Bulletin of Economic and Statistics, 52(2), 169-210. https://doi.org/10.1111/j.1468-0084.1990.mp52002003.x

(17) Khan, S., Faisal, M., Ul Haq, Z., Fahad, S., Ali, G., Khan, A., & Khan, I. (2019). Supply response of rice using time series data: Lessons from Khyber Pakhtunkhwa Province, Pakistan. Journal of the Saudi Society of Agricultural Sciences, 18(4), 458-461. https://doi.org/10.1016/j.jssas.2018.03.001

(18) Kohli, D. (1996). Supply response in agriculture: A review of methodologies. Working Papers No. 63. National Council of Applied Economic Research.

(19) Lutkepohl, H. (2005). New Introduction to Multiple Times Series Analysis. Springer.

(20) Mekbib, G., Kalkuhl, M., & von Braun, J. (2014). Agricultural supply response to international food prices and price volatility: a cross- country panel analysis. Center for Development Research.

(21) Mesike, C., Okoh, R., & Inoni, O. (2010). Supply response of rubber farmers in Nigeria: An application of vector error correction model. Agricultural Journal, 5(3), 146-150. http://dx.doi.org/10.3923/aj.2010.146.150

(22) Ministerio de Agricultura y Desarrollo Rural (2020). Cadena de plátano. https://sioc.minagricultura.gov.co/Platano/Documentos/2020-03-31%20Cifras%20Sectoriales.pdf

(23) Mose, L., Burger, K., & Kuvyenhoven, A. (2007). Aggregate supply response to price incentives: the case of smallholder maize production in Kenya. African Crop Science, 8, 1271-1275.

(24) Nerlove, M. (1958). Distributed lags and estimation of long-run supply and demand elasticities: Theoretical considerations. Agricultural and Applied Economics Association, 40(2), 301-311. https://doi.org/10.2307/1234920

(25) Nerlove, M. & Bessler, D. (2001). Expectation. Information and dynamics. Handbook of Agricultural Economics, 1(A), 155-206. https://doi.org/10.1016/S1574-0072(01)10006-X

(26) Quintero, J., & López, H. (2011). Respuesta de la oferta de arroz en Colombia 1994-2008. Revista Mundo Económico y Empresarial, (10), 60-72.

(27) Ramírez, M., González, F., Martínez, H., & Ortíz, L. (2004). Respuestas de la oferta y demanda agrícola en el marco de un TLC con Estados Unidos. Observatorio Agrocadenas, Documento de trabajo No. 49.

(28) Sánchez-Zuñiga, J., Sánchez-Molina, J., & Flórez-Vargas, A. (2020). Empleo del residuo agroindustrial del plátano como sustituto parcial del feldespato en la formulación de pasta de cerámica. Revista UIS de Ingeniería, 19(4), 157-166. https://doi.org/10.18273/revuin.v19n4-2020014

(29) Schwarz, G. (1978). Estimating the Dimension of a Model. The Annals of Statistics, 6(2), 461-464. https://doi.org/10.1214/aos/1176344136

(30) Sims, C. (1980). Macroeconomics and reality. Econometrica, 48, 1- 48. https://doi.org/10.2307/1912017

(31) Tripathi, A., & Prasad, A. (2009). Estimation of agricultural supply response by cointegration approach. The Indian Economic Journal, 57(1), 106-131. https://doi.org/10.1177/0019466220090106

(32) Van Wyk, D., & Treurnicht, N. (2012). A quantitative analysis of supply response in the Namibian mutton industry. South African Journal of Industrial Engineering, 23(1), 202-215.

Cómo citar este artículo: Cancino, S. y Cancino, G. (2021). Aplicación del modelo de ajuste parcial nerloviano para estimar la elasticidad de la oferta de plátano en Colombia. Tendencias, 22(2), 57-75. https://doi.org/10.22267/rtend.212202.168