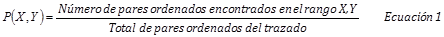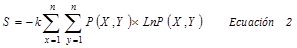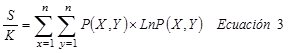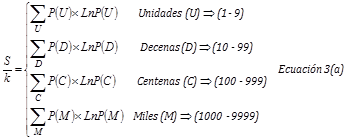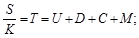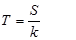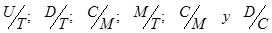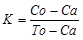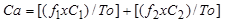Rodríguez-Velásquez, Prieto, and Ramírez-López: Dinámica cardiaca del adulto evaluada mediante las proporciones de la entropía

Introducción:

A partir de la teoría de los sistemas dinámicos, junto con la teoría de la probabilidad y el concepto de entropía se ha desarrollado una nueva metodología matemática de aplicación clínica.

Objetivo:

Aplicar la metodología previamente desarrollada para evaluar la dinámica cardíaca de adulto utilizando para ello la probabilidad y proporciones de la entropía del atractor.

Materiales y métodos:

Se desarrolló un estudio ciego tomando como Gold Standard el diagnóstico convencional emitido por un experto con 480 holter, 30 dinámicas normales y 450 con diferentes patologías; para cada holter se generó un atractor numérico cuantificando la probabilidad de aparición de parejas ordenadas de frecuencias cardiacas consecutivas, evaluando posteriormente la entropía, relación S/k y proporciones para cada dinámica durante mínimo 18 horas. Fueron hallados los valores de sensibilidad, especificidad y coeficiente Kappa.

Resultados:

La metodología aplicada permitió diferenciar cuantitativamente normalidad de enfermedad, encontrando los valores de las proporciones en los rangos establecidos. Los valores de sensibilidad y especificidad fueron de 100%, y el coeficiente Kappa fue de 1.

Conclusión:

A partir de las distribuciones de probabilidad de la aparición de parejas ordenadas de frecuencias cardiacas consecutivas y de su entropía es posible diagnosticar la dinámica cardiaca durante mínimo 18 horas.

Palabras clave: Electrocardiografía ambulatoria; matemática; dinámicas no lineales; frecuencia cardiaca.

Introduction:

A new mathematical methodology of clinical application has been developed from the theory of dynamic systems, together with the theory of probability and the concept of entropy.

Objective:

To apply the methodology previously developed to evaluate the heart dynamics of adult through the probability and proportions of entropy of the attractor.

Materials and methods:

A blind study was developed taking as Gold Standard the conventional diagnosis issued by an expert with 480 Holter, 30 normal dynamics and 450 with different pathologies. For each Holter, a numerical attractor was generated by quantifying the probability of appearance of consecutive pairs of cardiac frequencies, subsequently evaluating entropy, S/K ratio and proportions for each dynamic for at least 18 hours. The values of sensitivity, specificity and Kappa coefficient were found.

Results:

The applied methodology allowed to differentiate quantitatively normality of disease, finding the values of the proportions in the established ranges. The sensitivity and specificity values were 100%, and Kappa coefficient was 1.

Conclusion:

It is possible to diagnose cardiac dynamics for at least 18 hours based on the probability distributions of the appearance of consecutive pairs of cardiac frequencies and their entropy.

Keywords: Ambulatory electrocardiography, mathematics, nonlinear dynamics, heart rate

Introducción

El comportamiento de un sistema puede ser descrito a través del cambio temporal de las variables dinámicas de un sistema. Predecir y cuantificar este comportamiento a partir de las condiciones iniciales del sistema constituye el problema central de la teoría de los sistemas dinámicos¹^,². Las variables dinámicas del sistema son representadas de manera gráfica en el espacio de fase, recibiendo el nombre de atractores³. Si se observa en el espacio de fase un comportamiento irregular el atractor es caótico, este tipo de atractor se puede estudiar con la geometría fractal. Experimentos que pueden presentar un número finito de posibles eventos, pueden ser caracterizados a partir de la teoría de la probabilidad, la probabilidad permite cuantificar la posibilidad de ocurrencia de cada evento⁴. En cuanto a la entropía, ha sido redefinida en diferentes contextos, desde sus comienzos en el diseño de máquinas térmicas⁵^,⁶, en la teoría cinética de los gases, la mecánica estadística⁷ y en la inteligencia artificial⁸.

A nivel mundial, las enfermedades cardiovasculares (ECV) son consideradas la principal causa de muerte según la Organización Mundial de la Salud (OMS). Se estima que para el año 2012, 17,5 millones de personas murieron por esta causa, representando un 31% del total de muertes registras en el mundo. Más aún, tres de las cuartas partes de las defunciones por ECV se producen en los países con ingresos bajos y medios⁹^,¹⁰. Ante la situación presentada, el área de la cardiología ha visto en la necesidad de implementar nuevas estrategias con las cuales se pueda contribuir en la reducción de estos casos de mortalidad, planteando investigaciones encaminadas a mejorar los protocolos establecidos para el correcto seguimiento del paciente, así como mejorar los equipos biomédicos con los cuales se realiza el seguimiento del paciente.

El análisis de los registros electrocardiográficos continuos y/o Holter¹¹^-¹⁶, desde el contexto de la teoría de los sistemas dinámicos han reevaluado las nociones que se tiene frente a la variabilidad de la frecuencia cardiaca (FC) como parámetro de diagnóstico y predictor del comportamiento cardiaco. Es así, como las nuevas posturas enfocadas en la irregularidad de la dinámica cardiaca¹⁷^,¹⁸, desarrolladas en el marco de la teoría de los sistemas dinámicos, se han alejado de las concepciones convencionales de la regularidad, como ideal en la medicina derivadas de la noción de homeostasis. Las investigaciones hechas por Goldberger et al¹⁹., fundamentada en sistemas dinámicos no lineales, han encontrado que la dinámica cardiaca con un comportamiento excesivamente aleatorio o regular se asocia con casos patológicos, mientras que un comportamiento intermedio entre estos dos extremos se asocia con salud. En ese mismo contexto se han encontrado predictores más confiables de muerte por medio de dimensiones fractales en pacientes con Infarto Agudo de Miocardio (IAM) con fracción de eyección inferior al 35%²⁰. No obstante, la aplicabilidad clínica de estas dos últimas investigaciones aún no alcanza niveles plenamente satisfactorios requiriendo de estudios adicionales para confirmar y ajustar dicha aplicabilidad²¹^,²².

Otras investigaciones desarrolladas desde este mismo contexto, han dado origen a metodologías predictivas con las cuales es posible diagnosticar y hacer distinciones más precisas entre casos normales de enfermos, mediante parámetros matemáticos de aplicación clínica. Es así, como la dinámica cardiaca ha sido evaluada mediante los registros electrocardiográficos continuos y/o Holter durante 21, 16 y 15 horas¹¹^-¹⁶. En particular, la metodología fundamentada en la probabilidad y las proporciones de la entropía es un método de evaluación matemática de la dinámica cardiaca a partir de los registros Holter de pacientes mayores a 21 años, la cual permite

la predicción de diferencias entre normalidad, enfermedad crónica, enfermedad aguda y evolución entre estos estados. Esta metodología ha sido aplicada en varios estudios ciegos desarrollados para evaluar la dinámica cardiaca mediante registros Holter²³^-²⁵, en los cuales se ha encontrado que los valores de sensibilidad y especificidad fueron del 100%, y un coeficiente Kappa de 1.

La metodología ha permitido hacer precisiones matemáticas para dinámicas cardiacas de pacientes asintomáticos²⁶, logrando predecir la evolución a estados de agudización, a pesar de su imperceptibilidad desde parámetros clínicos convencionales. El propósito del presente trabajo es aplicar esta metodología¹¹ para evaluar dinámicas cardiacas normales y patológicas del adulto de manera cuantitativa, comparando esta evaluación con la evaluación clínica convencional, lo que permitirá confirmar la aplicabilidad clínica de la metodología.

Materiales y métodos

Definiciones

Tipo de estudio: Estudio de concordancia diagnóstica, de corte retrospectivo trasversal, por ello, al tratarse de la evaluación de una metodología matemática el estudio es independiente de los factores poblacionales como el sexo la edad y factores de riesgo, evitando así un sesgo de los resultados.

Mapa de retardo: Tipo de atractor específico que representa de manera gráfica la dinámica de un sistema, ubicando pares ordenados de valores de una variable dinámica consecutiva en el tiempo en un espacio de dos o más dimensiones.

Par ordenado de frecuencias cardiacas: Se define como cualquier combinación consecutiva de dos frecuencias cardiacas representadas como (x,y), las cuales estarán contenidas en el mapa de retardo, ubicándose en el rango de cinco, correspondiente de acuerdo a sus coordenadas.

Probabilidad de pares ordenados consecutivos en rangos de 5: Se define como el cociente entre la cantidad de pares ordenados que ocupen dicho rango y el total de pares ordenados de todo el trazado⁴⁾ (Ecuación 1)¹¹.

Entropía del atractor cardiaco

Se utilizará la expresión Boltzmann-Gibbs (Ecuación 2). Tenemos también la expresión para la relación S/k (Ecuación 3).

Donde S es la entropía, K la constate de Boltzman (1.38x10^-23 Joules/Kelvin), P(X, Y) es la probabilidad para cada rango (X, Y)²⁷^,²⁸. Se reorganiza la expresión para la Ecuación 3¹¹, en sumas parciales (Ecuación 3a)¹¹⁾ correspondientes al orden de magnitud de las frecuencias de aparición de los pares ordenados así:

Al incluir lo anterior en la Ecuación 3, se obtiene una simplificación que se puede observar en la Ecuación 4¹¹:

Donde

Proporciones entre las partes (U, D, C, M) y la totalidad (T) ⁽²⁷^,²⁸.

Las regiones del atractor previamente establecidas a evaluar son: la región 1, la cual contiene todos los rangos de la FC comunes almacenadas en los equipos Holter diagnosticadas como normales. La región 2, corresponde a la totalidad de los rangos ocupados por los registros Holter normales, excluyendo los de la región 1. La región 3, corresponde a la región restante total del mapa de retardo, es decir, los rangos de la FC que no son ocupados por los registros electrocardiográficos tipo Holter normales¹¹.

Población

Se tomó una totalidad de 480 registros Holter provenientes de la base de datos del grupo Insight, los cuales fueron evaluados por un cardiólogo experto que se encargó de establecer su diagnóstico desde los parámetros convencionales. Incluyendo patologías como diferentes tipos de arritmia, flutter, enfermedad coronaria, infarto agudo de miocardio, accidente cerebro vascular, comunicación interauricular.

Otros de los criterios de inclusión fueron que los holters provinieran de personas mayores de 21 años, y que mínimo tuvieran 21 horas de registro.

Procedimiento

De los registros Holter las conclusiones clínicas fueron enmascaradas y se tomaron los valores de la frecuencia cardiaca máximo y mínimo y el número de latidos para cada hora, durante 18 horas continuas. A partir de estos valores, para cada Holter, se desarrolló una simulación de la totalidad de la dinámica cardiaca, con la que se construyen parejas de frecuencias cardiacas consecutivas como se construyen para una mapa de retardo, con estos valores se generó un atractor numérico¹¹, para el que se tomó en cuenta la distribución de probabilidades de estas parejas ordenadas (Ecuación 1) organizadas en rangos de a 5 lat/min. Se hallaron posteriormente los valores de entropía (Ecuación 2).

Posteriormente, se aplicó la Ecuación 2 y Ecuación 3 a cada una de las dinámicas cardiacas evaluadas en 18 horas. Luego, fueron evaluadas las proporciones existentes entre cada sumando respecto a la totalidad (proporción S/k) y las proporciones entre centenas respecto a miles y decenas respecto a centenas para cada región determinada (Ecuación 4). Realizados todos estos pasos, se aplicaron los parámetros diagnósticos de la metodología desarrollada previamente¹¹, evaluando si por lo menos dos de las proporciones en cualquiera de las tres regiones están fuera de los límites de normalidad, lo cual es el parámetro diferenciador de anormalidad de normalidad.

Para cuantificar el nivel de gravedad de las dinámicas patológicas, tomando como referencia los valores extremos de la normalidad previamente definidos¹¹, a los valores de las proporciones que se encuentran por encima de estos límites se les restó el límite superior de normalidad, mientras que los valores inferiores al valor mínimo de normalidad fueron restados de dicho valor límite. Una vez obtenido el valor de estas diferencias, se suman según los órdenes de magnitud de unidades, decenas, centenas y miles con lo que finalmente, se cuantificó qué tan lejos o cerca se encuentran de la normalidad. Así, valores más altos correspondieron a patologías más agudas y valores menores a patologías menos severas.

Análisis estadístico

Para el desarrollo del estudio ciego, se obtuvo la evaluación matemática para cada uno de los 480 Holter. Seguidamente, se calculó la sensibilidad y especificidad de la presente metodología por medio de la comparación de la misma con los diagnósticos emitidos sobre los registros Holter por los especialistas expertos, los cuales son desenmascarados, asumiendo este diagnóstico como el Gold estándar. Para estos cálculos se denominaron verdaderos positivos (VP) a los casos que han sido diagnosticados como patológicos por ambas metodologías, falsos positivos (FP) a los casos que fueron evaluados matemáticamente como enfermos y por parte del experto clínico como normales. Los falsos negativos (FN) son los casos que fueron diagnosticados matemáticamente como normales pero que fueron catalogados por el experto como patológicos, y finalmente, los verdaderos negativos (VN) fueron los casos diagnosticados como dentro de límites normales por ambas metodologías. También se evaluó el coeficiente Kappa que determina la concordancia entre el diagnóstico físico-matemático y el diagnóstico convencional tomado como Gold Standard. Para esto se utiliza la Ecuación 5¹⁹:

En donde, Co representa el número de concordancias observadas que corresponden al número de pacientes con el mismo diagnóstico desde la metodología matemática y desde el Gold estándar; To representa la totalidad de casos; Ca corresponde al número de concordancias atribuibles al azar que se calculan a través de la siguiente Ecuación 5a¹⁹:

Donde f₁ equivale al número de casos con valores matemáticos de normalidad; C₁ representa el número de casos diagnosticados como normales por el experto clínico; f₂ representa el número de casos evaluados matemáticamente como enfermedad; C₂ representa el número de casos diagnosticados desde el ámbito clínico convencional con alguna patología; T_o representa el número total de casos.

Aspectos éticos

El presente estudio se declara como una investigación con riesgo mínimo, según la Resolución 8430 de 1993 del Ministerio de Salud colombiano, pues se realizan cálculos físicos y matemáticos sobre reportes de exámenes y paraclínicos no invasivos que han sido prescritos previamente según protocolos establecidos convencionalmente. Más aún, el estudio cumplió con los principios éticos de la Declaración de Helsinki de la Asociación Médica Mundial.

Resultados

Para las dinámicas cardiacas estudiadas los valores de entropía (Tabla 1) presentaron valores entre 4,567x 10^-23 y 7,0134x10^-23. Para los casos normales variaron entre 6,4512 x10^-23 y 7,013x 10^-23 y estos valores para las dinámicas enfermas variaron entre 4,3081x 10^-23 y 6,8765x 10^-23. Los valores de las proporciones de la entropía hallados para las dinámicas cardiacas normales varió entre 0 y 0,0325 para la U/T, entre 0 y 0,092 para D/T, entre 0 y 0,6177 para C/T, entre 0 y 0,856 para M/T, entre 0 y 3,348 para C/M y entre 0 y 9,1845 para D/C.

Las dinámicas cardiacas que presentaron valores más altos en las sumas de las restas de miles, corresponden a los estados patológicos agudos, mientras que otras patologías presentaron valores de miles más bajos, y los pacientes con arritmias y taquicardias presentaron los valores de miles más bajos de todos, sin embargo, no todas las arritmias presentaron valores bajos, como puede verse con los dos casos de arritmias descritos en la tabla, en el que la dinámica No. 5 presenta valores menores que la dinámica No. 24 (Tabla 2), mostrando que la metodología puede cuantificar diferentes grados de evolución de la enfermedad, que en la clasificación clínica convencional quedaría denominada bajo una misma clasificación que en este caso sería arritmia.

La aplicación de la metodología previamente desarrollada, reveló que la dinámica cardiaca evaluada con las proporciones de la entropía del atractor permite realizar distinciones cuantitativas entre dinámicas cardiacas normales de enfermas con registros de mínimo 18 horas.

Tabla 1. Diagnóstico clínico de 25 pacientes, tomados indiscriminadamente como muestra del total de la población

No.	Indicaciones	Proporción S/k	Entropía
1	Taquicardia, disminución de la variabilidad de la HR	-4,43021393	6,1137E-23
2	Enfermedad coronaria	-3,93223632	5,42649E-23
3	Enfermedad coronaria aguda	-3,4601161	4,77496E-23
4	Normal	-4,73575902	6,53535E-23
5	Arritmia	-4,29327814	5,92472E-23
6	Extrasístoles frecuentes, disminución moderada en la variabilidad de la frecuencia cardiaca.	-4,38004114	6,04446E-23
7	Enfermedad coronaria	-4,35084876	6,00417E-23
8	Arritmia cardiaca	-4,668116	6,442E-23
9	Comunicación intra auricular, dolor de pecho, mareo	-4,62572102	6,3835E-23
10	Síndrome Wolff-Parkinson-White, taquicardia por reentrada por vía accesoria	-4,64051815	6,40392E-23
11	Enfermedad coronaria	-4,44760309	6,13769E-23
12	Normal	-4,71731003	6,50989E-23
13	Incremento inapropiado de la frecuencia cardiaca, taquicardia sinusal.	-4,56522813	6,30001E-23
14	Taquicardia por reentrada nódulo AV	-4,6673261	6,44091E-23
15	Normal	-4,71984243	6,51338E-23
16	Flutter	-4,27173089	5,89499E-23
17	Normal	-4,7025305	6,48949E-23
18	Infarto agudo de miocardio	-3,5723367	4,92982E-23
19	Fibrilación auricular	-4,30146235	5,93602E-23
20	Marcapasos	-4,37019292	6,03087E-23
21	Enfermedad coronaria aguda	-3,48580713	4,81041E-23
22	Arritmia	-4,71444084	6,50593E-23
23	Infarto agudo de miocardio	-3,48067946	4,80334E-23
24	Arritmia	-4,62716169	6,38548E-23
25	Sincope	-4,42695822	6,1092E-23

Tabla 2. Valores de las proporciones de las partes y la totalidad de las tres regiones evaluadas y sumas

			Región 1						Región 2						Región 3					Sumas
N°	U/T	Tn/T	H/T	Th/T	H/Th	Tn/H	U/T	Tn/T	H/T	Th/T	H/Th	Tn/H	U/T	Tn/T	H/T	Th/T	H/Th	Tn/H	U:	D:	C:	M:
1	0,0003	0,0253	0,4997	0,4637	1,0776	0,0505	0,0003	0,0053	0,0055	0		0,9612	0	0	0	0			0,0001	0,0137	1,5298	0
2	0	0,039	0,3221	0,5738	0,5614	0,1211	0	0,0142	0,05	0		0,2845	0	0,0008	0	0			0	0,0008	2,3456	0,5474
3	0	0,0295	0,235	0,7259	0,3238	0,1256	0,0004	0,0021	0,0071	0		0,3017	0	0	0	0			0	0,0094	2,4066	0,937
4	0,0001	0,0855	0,4832	0,3108	1,5549	0,1769	0,0082	0,0845	0,0278	0		3,0427	0	0	0	0			0	0	0	0
5	0,0002	0,0209	0,4059	0,5662	0,7168	0,0516	0,0003	0,0017	0,0047	0		0,3701	0	0	0	0			0	0,018	2,1965	0,3843
6	0	0,0446	0,3963	0,5242	0,756	0,1124	0,0001	0,0313	0,0035	0		8,9706	0	0	0	0			0	0	5,7555	0,3031
7	0	0,0729	0,3207	0,5697	0,563	0,2273	0,0004	0,0269	0,0081	0		3,3002	0	0,0013	0	0			0	0,0013	0,1986	0,5416
8	0	0,0462	0,4259	0,4788	0,8897	0,1085	0,0041	0,0292	0,0138	0		2,1179	0,0002	0,0017	0	0			0,0002	0,0017	0,3994	0,124
9	0,0014	0,0227	0,5316	0,2997	1,7735	0,0428	0,0008	0,0219	0,0685	0,0224	3,0539	0,3198	0,0002	0,0168	0,0139	0		1,2129	0,0014	0,033	3,4334	0,9978
10	0,0002	0,0314	0,4248	0,5223	0,8134	0,0739	0	0,0173	0,004	0		4,3858	0	0	0	0			0	0,0076	1,149	0,2438
11	0	0,0405	0,3173	0,6314	0,5025	0,1277	0,0003	0,0053	0,0051	0		1,0309	0	0	0	0			0	0	1,5951	0,6638
12	0,0001	0,0894	0,4841	0,3138	1,543	0,1847	0,0083	0,0763	0,028	0		2,7238	0	0	0	0			0	0	0	0
13	0,007	0,0236	0,5764	0,2972	1,9392	0,041	0,0244	0,021	0,0399	0		0,5265	0,0025	0,0039	0,0041	0		0,9566	0,0252	0,0192	2,9596	0
14	0,0019	0,0272	0,519	0,3516	1,4761	0,0524	0,0007	0,0279	0,0578	0		0,4819	0,0026	0,0112	0	0			0,0043	0,023	2,0241	0
15	0	0,0874	0,4843	0,3139	1,5429	0,1806	0,0082	0,0781	0,0281	0		2,7806	0	0	0	0			0	0	0	0
16	0	0,0516	0,369	0,5372	0,687	0,1398	0,0008	0,0207	0,0207	0		1,004	0	0	0	0			0	0	1,5702	0,3851
17	0,0002	0,0393	0,4827	0,4557	1,0593	0,0814	0,0073	0,0112	0,0036	0		3,1031	0	0	0	0			0	0	0	0
18	0	0,0221	0,1708	0,8072	0,2116	0,1292	0	0	0	0			0	0	0	0			0	0,0184	0,3117	1,1305
19	0,0023	0,025	0,3622	0,577	0,6277	0,0689	0,0009	0,0249	0,004	0		6,2517	0,0004	0,0035	0	0			0,0025	0,0175	3,0825	0,4841
20	0,0009	0,042	0,3244	0,5971	0,5433	0,1294	0,0016	0,0227	0,0114	0		2,0009	0	0	0	0			0,0007	0	0,618	0,5887
21	0,0007	0,009	0,2739	0,707	0,3874	0,0328	0	0,0029	0,0065	0		0,4526	0	0	0	0			0,0005	0,03	2,2648	0,8545
22	0	0,0592	0,4529	0,431	1,0509	0,1307	0,0022	0,0355	0,0156	0		2,2704	0	0,0037	0	0			0	0,0037	0,22	0
23	0	0,0184	0,1782	0,8029	0,222	0,1033	0,0004	0	0	0			0	0	0	0			0	0,0221	0,3042	1,1158
24	0,0002	0,0815	0,3051	0,5303	0,5753	0,2673	0,0033	0,0574	0,0108	0		5,3141	0,001	0,0104	0	0			0,001	0,0104	2,2671	0,4899
25	0,0001	0,0568	0,3847	0,5268	0,7304	0,1476	0	0,0272	0,0044	0		6,1395	0	0	0	0			0	0	2,936	0,3313

[i] Sumas de las restas de los valores por fuera de los límites de normalidad agrupados de acuerdo con su orden de magnitud

Se desenmascararon los resultados de las conclusiones clínicas determinando que los valores para la especificidad y sensibilidad de las dinámicas cardiacas evaluadas fueron del 100% al comparar el diagnóstico matemático con el Gold estándar, de la misma manera el valor correspondiente a la concordancia entre el diagnóstico físico matemático y el diagnóstico clínico convencional, determinado mediante el coeficiente Kappa fue igual a 1. De este modo se confirma la aplicabilidad y reproductibilidad clínica de la metodología.

U/T, D/T, C/T, M/T, C/M, D/C: proporciones entre las partes y la totalidad definidas en la Ecuación 4, donde U: unidades, D: decenas, C: centenas, M: miles y T: totalidad. Sumas: corresponden a los valores de las proporciones por fuera de los límites de normalidad sumados de acuerdo con sus órdenes de magnitud obteniendo un valor asociado a unidades, decenas, centenas y miles.

Discusión

Este es el primer trabajo en el que mediante las proporciones de la entropía del atractor se logró evaluar la dinámica cardiaca de 480 holter durante mínimo 18 horas. El presente estudio de concordancia diagnóstica evidencia la posibilidad de realizar evaluaciones que determinen la condición clínica del paciente, mostrando que la metodología previamente desarrollada es aplicable para evaluar dinámicas cardiacas mínimo durante 18 horas, independientemente de factores poblacionales como sexo, factores de riesgo o edad (si es mayor a 21 años) ya que dicha información recopilada no incide al determinar el diagnóstico matemático. Teniendo en cuenta la comparación entre el diagnóstico convencional y la metodología matemática que se realiza con el análisis estadístico se observa que la concordancia diagnóstica fue máxima, estableciendo un valor de 1 para el coeficiente Kappa; para los valores de sensibilidad y especificada también se encontraron los mayores valores, ambas fueron del 100%, confirmando la aplicabilidad clínica de la metodología.

La estructura geométrica y numérica del atractor que se obtiene con la aplicación de esta metodología caracteriza el estado y la evolución temporal de la dinámica cardiaca, esta caracterización se logra a partir de las distribuciones espaciales de probabilidades de las parejas de frecuencias cardiacas, estableciendo proporciones que permiten evaluar cuantitativamente la dinámica cardiaca, mostrando diferencias objetivas entre dinámicas enfermas de normales, lo que podría ser de utilidad en la práctica clínica.

Otras metodologías fundamentadas como la teoría de los sistemas dinámicos, la geometría fractal y la teoría del caos, han logrado mediante la cuantificación de los espacios de ocupación de los atractores cardiacos medidos con el método de Box Counting, evaluar la dinámica cardiaca durante 16 horas, en pacientes ingresados a la Unidad de Cuidados Intensivos¹⁵. En este mismo escenario, se refinó la metodología mediante la aplicación de la teoría de conjuntos con la cual se pudo predecir casos de mortalidad, a partir de la evaluación de la dinámica cardiaca durante 15 horas¹⁶. Adicionalmente, la metodología reveló que el comportamiento de las variables analizadas en el laboratorio clínico a partir de la toma de gases arteriales y venosos, presenta un comportamiento caótico, diferenciable a partir de los valores máximos y mínimos ocupados por los atractores de estas variables¹⁶. Otra metodología, fundamentada en una ley matemática que evalúa la dinámica cardiaca caótica durante 21 horas, fue aplicada en casos con diagnóstico de arritmia, permitiendo cuantificar el grado de evolución hacia enfermedad aguda, así como ligeros cambios en la dinámica cardiaca que no son clasificados clínicamente como patológicos¹³.

En la literatura médica se encuentran estudios de tipo descriptivo en los cuales se analiza ciertos factores de riesgo que comprometen un correcto funcionamiento cardiaco²⁹^,³⁰. Debido a que un equipo Holter puede ser utilizado mientras se realizan actividades diarias, recientemente se realizó un estudio para evaluar la dinámica cardiaca de los bomberos de New York que se encuentran en servicio²⁹. Este y otros estudios de tipo descriptivo consideran los cambios de la variabilidad cardiaca como un predictor de eventos cardiacos³⁰ o muerte cardiaca²⁹. Sin embargo, cuando en estos estudios se encuentra otra patología cardíaca como puede ser una arritmia, requieren de nuevos estudios de tipo estadístico los cuales proporcionen variables de control específicas para prever cualquier eventualidad adversa, y garantizar un correcto seguimiento del funcionamiento cardiaco en este tipo de pacientes²⁹.

Los estudios fundamentados en metodologías cuyos análisis estadísticos son de tipo descriptivo y poblacional, permiten realizar afirmaciones sólo de la experiencia pasada, pues una de las características de la estadística es que es un cuerpo de métodos para aprender de la experiencia⁴⁴, la cual cambia y es específica por lo que no permite establecer generalizaciones. En cambio, el presente trabajo se apoya en la forma de proceder de la física teórica, en el que a partir de abstracciones e inducciones matemáticas del fenómeno, caracteriza el fenómeno de forma general mediante la formulación de teorías y leyes, que luego son aplicables a cada caso particular; prescindiendo de factores de riesgo o variables estadísticas.

Desde esta perspectiva se han desarrollado diferentes investigaciones que buscan establecer órdenes matemáticos en la medicina, con los cuales se puedan desarrollar metodologías predictivas. Dichas metodologías han logrado también evaluar la dinámica cardiaca neonatal, a partir de los registros Holter³¹, caracterizando tres momentos clave antes de presentarse las manifestaciones clínicas de sepsis³². También se ha evaluado la dinámica cardiaca de pacientes con implante de marcapasos, encontrando que las dinámicas cardiacas cuyos valores normales desde el ámbito clínico, la metodología los posiciona en rangos matemáticos de enfermedad³³. Adicionalmente, han desarrollado otras metodologías para áreas como son la morfometría arterial³⁴^,³⁵, celular³⁶^,³⁷, ventricular³⁸ y eritrocitaria³⁹; la infectología⁴⁰^,⁴¹, la epidemiología⁴², la biología molecular y la inmunología⁴³.

Conclusiones

El nuevo atractor numérico y geométrico basado en la aparición de parejas ordenadas de frecuencias cardiacas consecutivas, permite observar de manera más específica la dinámica para cada paciente.

Este nuevo tipo de atractor permite dar un contexto geométrico al concepto de entropía.

A partir de las distribuciones de probabilidad generadas a partir del atractor y de su entropía es posible diagnosticar matemáticamente la dinámica cardiaca durante mínimo 18 horas.

Agradecimientos

Agradecemos a la Universidad Militar Nueva Granada, por su apoyo a nuestras investigaciones. En especialmente agradecemos al Fondo de Investigaciones de la Universidad, a la Vicerrectoría de Investigaciones y la Facultad de Ingeniería por el soporte financiero prestado por medio del proyecto INV-ING-2096. Un agradecimiento especial a las Doctoras Marcela Guerrero, Vicerrectora de Investigaciones, Martha Bahamón, Vicerrectora Académica, Elsa Cárdenas, Directora del Centro de Investigaciones de la Facultad de Ingeniería, Laura Pramparo, Vicedecana de la Facultad de Ingeniería, José Duque, Decano de la Facultad de Ingeniería, Alejandro Castro, Jefe de la División de Investigación Científica.

De igual forma al Centro de Investigaciones de la Clínica del Country por apoyo a nuestras investigaciones; a los Doctores Tito Tulio Roa, Director de Educación Médica, Jorge Ospina, Director Médico, Alfonso Correa, Director del Centro de Investigaciones, y a las Doctoras Adriana Lizbeth, epidemióloga, Silvia Ortiz, Enfermera Jefe, y a Sandra Rodríguez, enfermera del Centro.

Conflicto de intereses: Ninguno declarado por los autores.

Referencias

1. Devaney RL, Siegel PB, Mallinckrodt AJ, McKay S. A first course in chaotic dynamical systems: theory and experiment. Comput Phys. AIP Publishing; 1993;7(4):416-7.

2. Peitgen HO, Jürgens H, Saupe D. Strange attractors, the locus of chaos. In: Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag; 1992. 655-768 p.

3. Calabrese JL. Ampliando las fronteras del reduccionismo. Deducción y Sist no lineales Psicoanálisis APdeBA. 1999;21(3):431-53.

4. Feynman RP, Leighton RB, Sands M. Probability. In: Physics Vol 1: Mechanics, radiation, and heat. Wilmington: Addison-Wesley Iberoamericana; 1964. p. 1-11.

5. Arrègle J. Procesos y tecnología de máquinas y motores térmicos. Valencia: Ed Univ Politéc; 2002.

6. Feynman RP, Leighton RB, Sands M. The Laws of Thermodynamics. In: Physics Vol 1: Mechanics, radiation, and heathysics. Wilmington: Addison-Wesley Iberoamericana; 1964. p. 1-13.

7. Frodden E, Royo J. Entropía e información, Seminario Final del curso de Termodinámica, Depto. de Física, Facultad de Ciencias, Universidad de Chile. Chile: Universidad de Chile; 2004.

8. Shore JE. Relative entropy, probabilistic inference and AI. Washington: Computer Science and Systems Branch; 2013.

9 Organizacion Mundial de la Salud. Centro de prensa. Enfermedades cardiovasculares [Internet]. Ginebra: OMS; 2015.[cited 2017 Jul 10]. Available from: http://www.who.int/mediacentre/factsheets/fs317/es/

10. Mozaffarian D, Benjamin EJ, Go AS, Arnett DK, Blaha MJ, Cushman M, et al. Heart disease and stroke statistics-2015 update?: A report from the American Heart Association. Circulation. 2015;131(4):e29-322.

11. Rodríguez J. Entropía proporcional de los sistemas dinámicos cardiacos. Predicciones físicas y matemáticas de la dinámica cardiaca de aplicación clínica. Rev Colomb Cardiol. 2010;17(3):115-29.

12. Rodríguez J, Prieto S, Correa C, Bautista J, Velasco A, Mendez L, et al. Mathematics physical assessment of cardiac dynamics based on theory of probability and proportions of entropy in the Intensive care Unit for patients with arrhythmia. In: International Conference on Medical Phyiscs; 2015 Birmingham. Journal of Nuclear Medicine & Radiation Therapy; 2015.

13. Rodríguez J. Mathematical law of chaotic cardiac dynamics: Predictions for clinical application. J Med Med Sci. 2011;2(8):1050-9.

14. Rodríguez-Velásquez J, Prieto S, Domínguez D, Correa C, Melo M, Pardo J, et al. Application of the chaotic power law to the study of cardiac dynamics in patients with arrhythmias. Rev fac med. 2014;62(4):539-546.

15. Colombiana De A, Rodríguez J, Prieto S, Correa C, Oliveros H, Soracipa Y, et al. Diagnóstico físico-matemático de la dinámica cardiaca a partir de sistemas dinámicos y geometría fractal: disminución del tiempo de evaluación de la dinámica cardiaca de 21 a 16 horas. Acta Colomb Cuid Intensivo. 2016;16(1):15-22.

16. Rodríguez Velásquez J. Dynamical systems applied to dynamic variables of patients from the intensive care unit (ICU): Physical and mathematical mortality predictions on ICU. J Med Med Sci. 2015;6(8):209-20.

17. Wu GQ, Arzeno NM, Shen LL, Tang DK, Zheng DA, Zhao NQ, et al. Chaotic signatures of heart rate variability and its power spectrum in health, aging and heart failure. PLoS One. 2009;4(2):e4323.

18. Braun C, Kowallik P, Freking A, Hadeler D, Kniffki KD, Meesmann M. Demonstration of nonlinear components in heart rate variability of healthy persons. Am J Physiol Circ Physiol. Am Physiological Soc; 1998;275(5):H1577-84.

19. Goldberger AL, Amaral LAN, Hausdorff JM, Ivanov PC, Peng CK, Stanley HE. Fractal dynamics in physiology: Alterations with disease and aging. Proc Natl Acad Sci. 2002;99(Suppl 1):2466-72.

20. Huikuri H, Makikällo T, Peng Ch, Goldberger A, Hintze U, Moller M. Fractal correlation Properties of R-R Interval Dynamics and Mortality in Patients with Depressed Left Ventricular Function After an Acute Miocardial Infarction. Circulation. 2000;101(1):47-53.

21. Perkiömäki JS, Mäkikallio TH, Huikuri H V. Fractal and Complexity Measures of Heart Rate Variability. Clin Exp Hypertens. Taylor & Francis; 2005 Jan 1;27(2-3):149-58.

22. Voss A, Schulz S, Schroeder R, Baumert M, Caminal P. Methods derived from nonlinear dynamics for analysing heart rate variability. Philos Trans R Soc A Math Phys Eng Sci. 2009;367(1887):277-96.

23. Rodríguez J, Prieto S, Domínguez D, Melo M, Mendoza F, Correa C, et al. Mathematical-physical prediction of cardiac dynamics using the proportional entropy of dynamic systems. J Med Med Sci. 2013;4(9):370-81.

24. Rodríguez J, Prieto S, Correa C, Soracipa Y, Mora J, Bernal P, et al. Predicciones de la entropía proporcional en la dinámica cardiaca. Rev fac Med. 2015;23(2):60-70.

25. Rodríguez J, Prieto S, Correa C, Soracipa Y, Aguirre G, Méndez L. Proportional entropy applied to the clinical diagnostic of cardiac dynamic: blind study with 600 holter. In: 61st Annual Conference of the Israel Heart Society in association with The Israel Society of Cardiothoracic Surgery; 2014 Israel. Tel Aviv; 2014.

26. Rodríguez J, Prieto S, Bernal P, Isaza D, Salazar G, Correa C, et al. Entropía proporcional aplicada a la evolución de la dinámica cardiaca. Predicciones de aplicación clínica. In: Rodríguez L, editor. La emergencia de los enfoques de la complejidad en América Latina Tomo I. Buenos Aires: Comunidad Editora Latinoamericana; 2016. p. 315-34.

27. Matvéev AN. Física molecular. Moscú: MIR; 1987.

28. Tolman R. Principles of statistical mechanics. 1st ed. New York: Dover Publications; 1979. 662 p.

29. Al-Zaiti SS, Carey MG. The prevalence of clinical and electrocardiographic risk factors of cardiovascular death among on-duty professional firefighters. J Cardiovasc Nurs. NIH Public Access; 2015;30(5):440.

30. Carey MG, Thevenin BJM. High resolution 12-lead electrocardiograms of on-duty professional firefighters: a pilot feasibility study. J Cardiovasc Nurs. NIH Public Access; 2009;24(4):261.

31. Rodríguez-Velásquez J, Prieto-Bohórquez S, Flórez-Cárdenas M, Alarcón-Ávila C, López-Cruz R, Aguirre-Dávila G, et al. Cardiac dynamic systems in normal neonates: Neonate chaotic cardiac law. Rev Salud Uninorte. Fundación Universidad del Norte; 2014;30(3):361-70.

32. Rodríguez J, Prieto S, Flórez M, Alarcón C, López R, Aguirrre G, et al. Physical-mathematical diagnosis of cardiac dynamic on neonatal sepsis: predictions of clinical application. J Med Med Sci. 2014;5(5):102-8.

33. Rodríguez J, Prieto S, Correa C, Bernal P, Vitery S, Alvarez L, et al. Diagnóstico cardiaco basado en la probabilidad aplicado a pacientes con marcapasos. Acta Med Colomb. 2012;37(4):183-91.

34. Rodríguez JO, Prieto SE, Correa C, Bernal PA, Puerta GE, Vitery S, et al. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Med Phys. 2010;10:1-6.

35. Rodríguez J, Prieto S, Correa C, Polo F, Soracipa Y, Blanco V, et al. Fractal and euclidean geometric generalization of normal and restenosed arteries. J Med Med Sci. 2013;4(4):174-80.

36. Prieto Bohórquez SE, Velásquez JOR, Correa Herrera SC, Soracipa Muñoz MY. Diagnosis of cervical cells based on fractal and Euclidian geometrical measurements: Intrinsic Geometric Cellular Organization. BMC Med Phys. 2014;14(1):2.

37. Rodríguez Velásquez J, Prieto Bohórquez S, Correa SC, Domínguez Cajeli D, Cardona Velásquez DM, Melo De Alonso M. Geometrical nuclear diagnosis and total paths of cervical cell evolution from normality to cancer. J Cancer Res Ther. 2015;11(1):98-104.

38. Rodríguez Velásquez J, Prieto S, Correa C, Soracipa Y, Mora J, Forero M, et al. Generalización geométrica fractal de ventriculografías izquierdas normales y con disfunción leve. Acta Med Colomb. 2014;39(2):131-136.

39. Rodríguez J, Prieto S, Correa C, Mejía M, Ospino B, Munevar Á, et al. Simulación de trayectorias de alteración de estructuras eritrocitarias con base en la geometría fractal y euclidiana. Arch Med. 2014;14(2):267-284.

40. Rodríguez JO, Prieto SE, Correa C, Pérez CE, Mora JT, Bravo J, et al. Predictions of CD4 lymphocytes' count in HIV patients from complete blood count. BMC Med Phys. 2013;13:1.

41. Rodríguez J, Prieto S, Melo M, Domínguez D, Correa C, Soracipa Y, et al. Predicción del número de linfocitos T CD4 en sangre periférica a partir de teoría de conjuntos y probabilidad en pacientes con VIH/SIDA. Inmunología. Elsevier; 2014;33(4):113-20.

42. Rodríguez Velásquez J. Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev Panam Salud Publica. 2010;27(3):211-8.

43. Rodríguez J. Teoría de unión al HLA clase II: teoría de probabilidad, combinatoria y entropía aplicadas a secuencias peptídicas. Inmunología. Elsevier; 2008;27(4):151-66.

44. Moses LE. Statistical concepts fundamental to investigations. In: Bailar JCI, Hoaglin DC, editors. Medical Uses of Statistics. 3rd ed. Hoboken: John Wiley & Sons; 2009. 5-26 p.

Dinámica cardiaca del adulto evaluada mediante las proporciones de la entropía

Adult dynamic heart evaluated by the proportions of entropy

Resumen