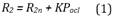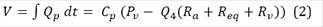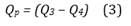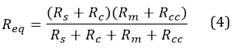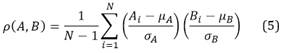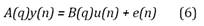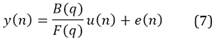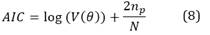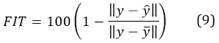Modelado del sistema cardiovascular para evaluación de técnicas de estimación de reactividad vascular basadas en hiperemia reactiva

Translated title (en): Modeling of cardiovascular system for evaluation of vascular reactivity estimation techniques based on reactive hyperemia
Diana Carolina Arboleda-Gómez 1 , Jenny Kateryne Aristizábal-Nieto 1 , Alher Mauricio Hernández-Valdivieso 1
 

[1] Grupo de Investigación en Bioinstrumentación e Ingeniería Clínica - GIBIC, Programa de Bioingeniería, Universidad de Antioquia. Medellín, Colombia. Universidad de Antioquia Grupo de Investigación en Bioinstrumentación e Ingeniería Clínica - GIBIC Programa de Bioingeniería Universidad de Antioquia Medellín Colombia

Author notes:
Correspondence to: Autor de correspondencia: Alher Mauricio Hernández Valdivieso. e-mail: alher.hernandez@udea.edu.co

Resumen

Introducción:

La evaluación de la reactividad vascular (RV) se hace mediante la respuesta hiperémica después de una isquemia producida por oclusión arterial. Existen técnicas de medición de RV que permiten evaluar la función vascular con menor costo y sin dependencia del operador, pero se encuentran en desarrollo y requieren validación y aceptación clínica.

Objetivo:

Modelar computacionalmente la mecánica vascular con el fin de evaluar el desempeño de una técnica de RV.

Materiales y métodos:

Se modificó el modelo eléctrico de la vasculatura del brazo, obteniendo el volumen periférico con y sin oclusión de la arteria braquial. Se realizó una identificación computacional que relaciona el volumen periférico con los resultados de una técnica de evaluación de RV que presenta cambios de color en la mano ocluida durante hiperemia reactiva. El software utilizado fue Matlab(r).

Resultados:

El modelo modificado permitió obtener el volumen periférico con y sin oclusión representando la perfusión en la microvascultura. El modelo no lineal Hammerstein-Weiner fue el mejor descriptor de los cambios de color en función de la dinámica del sistema vascular y presentó porcentaje de ajuste promedio de 95,69%.

Conclusiones:

Es posible modelar computacionalmente la técnica de evaluación de la función vascular utilizando identificación no lineal.


Keywords: Cardiovascular diseases, hyperemia, biological models, computer simulation

Abstract

Introduction:

The evaluation of vascular reactivity (VR) is done by the hyperemic response after ischemia produced by arterial occlusion. There are VR measurement techniques that allow the evaluation of vascular function at lower cost and without dependence on the operator, but they are in development and require validation and clinical acceptance.

Objective:

To model vascular mechanics computationally in order to evaluate the performance of a VR technique.

Materials and methods:

The electrical model of the vasculature of the arm was modified, obtaining the peripheral volume with and without brachial artery occlusion. A computational identification, which relates the peripheral volume to the results of a VR evaluation technique and presents color changes in the occluded hand during reactive hyperemia, was performed. The software used was Matlab(r).

Results:

The modified model allowed to obtain the peripheral volume with and without occlusion, representing the perfusion in the microvasculature. The Hammerstein-Weiner non-linear model was the best descriptor of color changes depending on the dynamics of the vascular system and it presented an average adjustment percentage of 95.69%.

Conclusions:

It is possible to model computationally the technique of evaluation of vascular function using nonlinear identification.


Keywords: Cardiovascular diseases, hyperemia, biological models, computer simulation

Introducción

Las enfermedades cardiovasculares (ECV) constituyen una de las causas más importantes de discapacidad y muerte prematura en todo el mundo; en 2012 murieron por esta causa 17,5 millones de personas, correspondiente al 31% de todas las muertes registradas1.

Actualmente, las estrategias preventivas contra las ECV son el centro de interés en las investigaciones médicas2. En diversas investigaciones se ha evidenciado que el deterioro de la función vascular es el paso inicial en el desarrollo de complicaciones cardiovasculares2-4, por tanto, es importante que, como primer paso en la detección o evaluación de riesgo de las ECV, se evalúe la reactividad vascular (RV).

Los estudios de la función vascular se conocen como pruebas de RV5; los cuales pueden ser un método efectivo para diagnosticar el daño vascular. La RV medida en una arteria es extrapolable a la de otras arterias en el mismo sujeto6; con base en esta premisa, la técnica más usada para estudiar la RV es medir la respuesta hiperémica después de una isquemia producida por oclusión arterial4,5.

Un método estándar para la evaluación de la función vascular es la dilatación mediada por flujo (FDM, por sus siglas en inglés) de los vasos, basada en el efecto de vasodilatación que produce el incremento del flujo sanguíneo, y se mide el cambio máximo porcentual en el diámetro arterial, mediante imágenes de ultrasonido de alta resolución7. Una de las limitaciones del método es la dependencia de las habilidades del operador que captura la imagen de la arteria y el alto costo del equipo de ultrasonido de alta resolución. Por lo tanto, se han realizado esfuerzos para evaluar el estado vascular durante la hiperemia reactiva (HR) mediante técnicas menos dependientes del operador y menos costosas.

Ante esta situación han surgido nuevas técnicas diagnósticas que evalúan RV mediante HR en una extremidad5,8-14, las cuales buscan un promisorio avance en la detección temprana de las ECV, sin embargo estos métodos se encuentran en estado de desarrollo y requieren validación y aceptación clínica.

Actualmente, el Grupo de Investigación en Bioinstrumentación e Ingeniería Clínica, GIBIC, en asocio con el Grupo de Investigación en Fisiología y Bioquímica, PHYSIS, de la Universidad de Antioquia, investigan sobre una técnica para evaluar la función vascular mediante los cambios de color de las manos durante la HR. El resultado entregado por el dispositivo está compuesto de tres curvas por cada componente de color, que relacionan la mano control respecto a su contralateral ocluida, antes, durante y después de la isquemia inducida. Aun cuando se puede inferir que el cambio de color de la mano con el vaso ocluido está relacionado con los cambios en la perfusión sanguínea, interesa entender con mayor detalle los cambios ocurridos en la vasculatura durante la HR y su relación desde el punto de vista fisiológico con los cambios de color observados.

Una alternativa para lograr este entendimiento es el modelado computacional y para tal fin se propone como hipótesis de trabajo, que es posible modelar computacionalmente la mecánica vascular y el proceso asociado de cambios de coloración en las palmas de las manos durante la HR. Un modelo de estas características permitiría identificar qué parámetro mecánico de la vasculatura varía cuando se detectan cambios específicos de coloración en la palma de las manos.

Un estudio de la extremidad superior de la mano y el proceso de oclusión fue implementado por Goldoozian et al.15, quienes aplicaron un modelo agrupado desde el extremo de la aorta ascendente hasta la microvasculatura del pulpejo dactilar; donde cada segmento vascular fue modelado mediante un circuito eléctrico RLC (resistencia, inductor y capacitor). El brazalete de oclusión fue implementado mediante un interruptor (SW), en el que la posición abierta del SW representa la oclusión del brazo. La salida del modelo es el volumen periférico durante todo el proceso de HR. La ventaja de este es que se ha utilizado previamente para modelar diferentes mecanismos reguladores incluyendo la función endotelial16,17.

En este artículo se presenta la modificación del modelo de la vasculatura previamente reportado en la literatura, que permite establecer la relación entre el volumen periférico y los cambios de color

de las manos antes, durante y después de la oclusión arterial. Para tal fin se presenta la modificación del modelo, las técnicas de identificación empleadas, los resultados obtenidos y posteriormente se discute su utilidad frente a los procesos de validación de técnicas de estimación de la RV.

Materiales y métodos

Modelo computacional

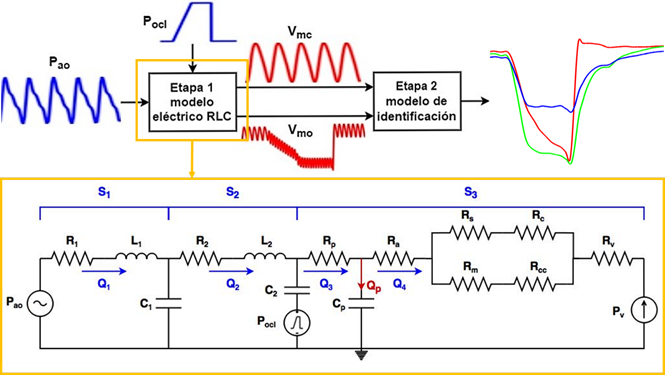
El modelo propuesto está compuesto por dos etapas, la primera es una modificación del modelo de predicción implementado por Goldoozian et al.15, y la segunda es el modelo resultante del proceso de identificación propuesto en este artículo. En la figura 1 se presenta el esquema general en donde se pueden ver cuáles son las entradas y salidas de cada subsistema.

Figura 1. Arriba: Esquema general del modelo propuesto. Abajo, ampliación del recuadro naranja: Analogía eléctrica de la extremidad superior con el brazalete de oclusión. Modificación propuesta para el modelo de Goldoozian et al.15 con el fin de simular oclusión con brazalete. Pao presión en la aorta, Pocl presión de oclusión, Vmc volumen periférico de la mano control, Vmo volumen periférico de la mano ocluida, R1 resistencia de la aorta ascendente, L1 inercia de la aorta ascendente, C1 distensibilidad de la aorta ascendente, R2 resistencia del brazo, L2 inercia del brazo, C2 distensibilidad del brazo, Rp resistencia de las arterias terminales, Cp distensibilidad de las arterias terminales, Ra resistencia de las arteriolas grandes, Rm y Rs resistencia de las arteriolas pequeñas, Rc y Rcc resistencia de los capilares, Rv resistencia de las vénulas, y Pv la presión a la entrada venosa.
0124-7107-reus-20-02-00139-gf1.png

Primera etapa: Modelo eléctrico RLC

Corresponde al propuesto por Goldoozian et al.15, donde las ecuaciones resultan del análisis de circuitos aplicados a la analogía eléctrica del sistema vascular de la extremidad superior; cada segmento arterial fue modelado como un vaso cilíndrico con paredes viscoelásticas no extensible en la dirección longitudinal18, mediante un circuito eléctrico RLC. El parámetro R describe la resistencia al flujo que percibe la sangre, C se refiere a la distensibilidad de la arteria, y L representa la inercia de la sangre; además la presión (P) sería análoga al voltaje y el flujo sanguíneo (Q) a la corriente eléctrica15,19.

La señal de entrada al sistema está dada por la presión en la aorta (Pao). Pao es obtenida mediante una serie de Fourier que reconstruye la forma de onda de la presión sanguínea en función del tiempo, la frecuencia cardiaca, la presión arterial sistólica (Psis), presión arterial diastólica (Pdia) y la presión de pulso20. Los valores simulados de Psis/Pdia fueron 80/120 mmHg. Así mismo, la frecuencia cardiaca fue de 70 veces por minuto en condiciones de reposo21.

La modificación propuesta al modelo de Goldoozian et al.15, en la ampliación del recuadro naranja, donde S1 corresponde el segmento desde la aorta ascendente hasta la posición del brazalete, S2 modela el resto del brazo hasta la entrada periférica y S3 es la red periférica (Figura 1).

La modificación permite representar la acción del brazalete de oclusión, a través del cambio en el tiempo de la resistencia del brazo (R2) mediante una señal de oclusión (Pocl) multiplicado por un factor K. También el nivel de referencia de la distensibilidad del brazo (C2) se ve afectada por Pocl. La señal de Pocl fue modelada con una señal rampa, que comienza a incrementar en el momento de inicio de la oclusión hasta alcanzar un valor de 20 mmHg por encima de la Psis, sosteniendo este último valor hasta la liberación del brazalete, y retorna a cero. Mientras Pocl se encuentra en cero, R2 es igual al valor nominal (R2n) y el circuito se comporta como el sistema presentado por Goldoozian et al.15. La ecuación que describe el comportamiento de R2 para simular presiones aplicadas por el brazalete se da en la siguiente expresión:

0124-7107-reus-20-02-00139-ee1.jpg

Los valores de los elementos eléctricos del modelo de la Figura 1 (ampliación del recuadro naranja) dependen de las propiedades reológicas de la sangre, los parámetros geométricos y mecánicos del segmento del vaso, y el número de vasos16,17. Los valores nominales de cada elemento eléctrico del modelo son: resistencia de la aorta ascendente (R1) igual a 1.26k mmHg.s.l-1, inercia de la aorta ascendente (L1) igual a 27 mmHg.s2.l-1, distensibilidad de la aorta ascendente (C1) igual a 66.67μ l.mmHg-1, resistencia del brazo (R2n) igual a 3.17k mmHg.s.l-1, inercia del brazo (L2) igual a 369 mmHg.s2.l-1, distensibilidad del brazo (C2) igual a 6𝜇 l.mmHg-1, resistencia de las arterias terminales (Rp) igual a 17.73k mmHg.s.l-1, distensibilidad de las arterias terminales (Cp) igual a 4.8𝜇 l.mmHg-1, resistencia de las arteriolas grandes (Ra) igual a 40.2k mmHg.s.l-1, resistencia de las arteriolas pequeñas (Rm, Rs) igual a 701.03k mmHg.s.l-1, resistencia de los capilares (Rc, Rcc) igual a 3.195k mmHg.s.l-1, y resistencia de las vénulas (Rv) igual a 27.9k mmHg.s.l-1. La presión Pv corresponde a la entrada venosa y se estableció en 8 mmHg, de acuerdo con el rango de valores fisiológicos15-17.

La salida entregada por el modelo es el volumen periférico, calculado a partir de la integral del flujo periférico Qp (Figura 1). Las ecuaciones del modelo fueron implementadas en Matlab(r) y Simulink(r). El modelo es simulado en dos ocasiones, la primera para obtener la señal de volumen periférico de la mano control (Vmc) con la Pocl en cero, y en la segunda para registrar la señal de volumen periférico para la mano ocluida (Vmo) con Pocl en funcionamiento. Las ecuaciones (2), (3) y (4) obtenidas a partir del modelo, calculan dichos volúmenes periféricos.

0124-7107-reus-20-02-00139-ee2.jpg

Donde:

0124-7107-reus-20-02-00139-ee3.jpg

0124-7107-reus-20-02-00139-ee4.jpg

El volumen V depende de Q3 y Q4, y estos a su vez se ven afectados por el funcionamiento de Pocl. Mientras Pocl está en cero, V se comporta como Vmc y cuando Pocl se encuentra activa, V es igual a Vmo.

Para identificar el valor del parámetro K en la ecuación 1, se implementó un proceso de identificación con el fin de ajustar la salida de la primera etapa del modelo a una señal de presión adquirida experimentalmente.

Segunda etapa: Modelo de identificación

El modelo que relaciona los cambios de volumen vascular (perfusión sanguínea) con los cambios de color de las palmas de la mano, corresponde a un problema de identificación de tipo caja negra, en donde solo son conocidas las señales de entrada y salida del modelo. Vmc y Vmo (volumen en la microvasculatura de las manos, sin oclusión y con oclusión, respectivamente) calculadas a partir de la simulación de la primera etapa y corresponden a las entradas de esta etapa.

Las salidas del sistema dependen de la técnica implementada para realizar la medida de RV. En este caso se trata de la comparación del cambio de coloración de las dos manos y para tal fin, la forma más sencilla de identificar un cambio de coloración es utilizar la correlación cruzada entre los cambios de color en las tres componentes Rojo, Verde y Azul (RGB, por sus siglas en inglés). Es así, como cada secuencia de imágenes capturada por una cámara son desagregadas en sus componentes de color y posteriormente se calcula la correlación entre los tres pares de secuencias (mano ocluida y mano control), utilizando el coeficiente de correlación lineal de Pearson22, así:

0124-7107-reus-20-02-00139-ee5.jpg

Donde A y B son dos variables aleatorias, N es el número de observaciones, μA y σA son la media y la desviación estándar de A, y μB y σB son la media y la desviación estándar de B, respectivamente.

Dado que el coeficiente de Pearson calculado con la ecuación (5) cambia para cada par de imágenes, se obtiene una serie de coeficientes para cada componente de color que describe el cambio de coloración. Cada una de las tres curvas de cambio de color corresponde a una señal de salida del sistema de caja negra, de tal forma que se cuenta con tres curvas de salida que representan el cambio de la mano ocluida con respecto a su bilateral control, durante el proceso de hiperemia reactiva (antes, durante y después de la oclusión de la arteria braquial).

Datos experimentales

Con el propósito de validar los resultados de la etapa 2 (Figura 1), es decir, las curvas de cambio de color, se realizó una prueba experimental de medición de la RV con el equipo desarrollado por el grupo de investigación, dicha prueba forma parte de un estudio descriptivo. El estudio se realizó en un sujeto sano sin problemas de presión arterial, sin enfermedad cardiovascular evidente, sin obesidad, y que no consume medicamentos que puedan afectar al sistema cardiovascular. El día de la prueba, el voluntario no realizó ejercicio, no fumó, y no consumió cafeína ni alcohol. Para el momento de la prueba, el sujeto se presentó con las manos limpias, sin accesorios en los dedos, en estado de reposo y sin agitación.

Una vez dispuesto un brazalete de oclusión en el brazo del sujeto, y ubicadas las manos en posición de pronación sobre la superficie de grabación, se inició el registro del video de la palma de ambas manos con la cámara. Luego de transcurridos 40s en los cuales se tomó una línea de base del video, se generó un estímulo isquémico mediante la oclusión de la arteria braquial por medio del inflado del brazalete, calculando simultáneamente la presión Psis y Pdia, y manteniendo sostenida una presión de oclusión (Psis + 20 mmHg), por un tiempo máximo de dos min. Luego, la presión sostenida fue liberada inmediatamente, y como consecuencia se dio una respuesta hiperémica, debido a la recuperación de la isquemia, la cual fue grabada durante 3 min. En paralelo al proceso mencionado, se evaluaron los cambios de color en la palma de las manos control y prueba, antes, durante y después del estímulo isquémico inducido, comparando ambas manos mediante el coeficiente de correlación de Pearson y obteniendo como resultado curvas de cambio de color para cada espacio rojo, verde y azul, como se presenta en la salida de la etapa 2 (Figura 1).

Identificación paramétrica del sistema correspondiente a la segunda etapa

La identificación del sistema se realizó utilizando Matlab(r) mediante estructuras paramétricas que relacionan las señales de interés del sistema (entradas, salida y perturbaciones). La primera característica para identificar en el sistema es el orden del retardo (nk), que deberá corresponder a la situación física de interés, teniendo en cuenta que la frecuencia de muestreo es 21 Hz y que cambios en la presión de entrada deben producir cambios de color en la mano en cada latido, los retardos deberán estar alrededor de nk=21.

Se utilizaron estructuras de identificación lineales autorregresivas con entrada exógena (ARX, por sus siglas en inglés) y error en la salida (OE, por sus siglas en inglés) que se representan respectivamente por las siguientes expresiones23:

0124-7107-reus-20-02-00139-ee6.jpg

0124-7107-reus-20-02-00139-ee7.jpg

En las ecuaciones (6) y (7), la señal u(n) corresponde a las dos señales de entrada (Vmc y Vmo), A(q), B(q) y F(q) representan los polinomios de regresión de la salida y entrada. Los órdenes de dichos polinomios deberán permitir capturar la dinámica del sistema, por tal razón se prueban órdenes (na, nb, nf y nk) tales que, teniendo en cuenta la frecuencia de muestreo de los datos experimentales, sea posible representar la dinámica de la señal de salida. Después de una exploración de los datos experimentales, se encontró que órdenes inferiores a 30 permiten representar dichas señales.

El criterio usado para medir la calidad del modelo obtenido es conocido como el criterio de información de Akaike (AIC, por sus siglas en inglés), donde el modelo más preciso tiene el AIC más pequeño que se define como 24:

0124-7107-reus-20-02-00139-ee8.jpg

Donde

0124-7107-reus-20-02-00139-ee10.jpg

Es la función de pérdida, np es el número de parámetros en el modelo y N es el número de muestras de los datos.

La bondad de ajuste entre los datos experimentales y los predichos es calculado mediante el porcentaje de ajuste (FIT), como se presenta en la siguiente expresión23:

0124-7107-reus-20-02-00139-ee9.jpg

Donde 𝑦 es la señal de salida experimental, 𝑦 la salida predicha del modelo y 𝑦 es la media de 𝑦. Con el fin de verificar si asumir una estructura no lineal para esta etapa podría proporcionar mejores resultados, una vez identificado el mejor sistema lineal que reproduce las señales de salida, se procedió a la implementación de un modelo de identificación no lineal mediante la estructura Hammerstein-Weiner (HW)25,26 utilizando como componente lineal los polinomios del mejor modelo obtenido.

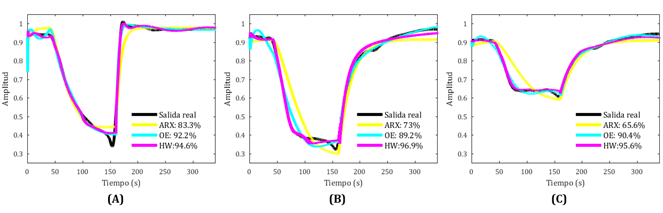
Esta estrategia de identificación proporcionará una estructura y sus órdenes respectivos por cada curva de color, es decir, tres modelos en total, cada uno con dos entradas y una salida (MISO, por sus siglas en inglés).

Consideraciones éticas

La realización de la prueba experimental de medición de la RV fue avalada por el Comité de Ética en Investigación de la Clínica Medellín.

Resultados

Primera etapa: Volúmenes obtenidos a partir del modelo eléctrico RLC

En la salida de la etapa 1 (Figura 1) se presentan las formas de onda de los volúmenes periféricos, Vmc y Vmo, obtenidos a partir de la ecuación 2, luego de simular el modelo de la primera etapa. El valor de K presentado en la ecuación 1 es un factor desconocido en el modelo, por esto se tomó un valor inicial que permitiera obtener señales de volumen con buen sentido fisiológico, es decir, que representara valores positivos de la curva. De este modo, se eligió K=1500 para realizar los cálculos.

Segunda etapa: Modelo de identificación

Los resultados de la segunda etapa del modelo de identificación mediante las estructuras ARX, OE se presentan según los órdenes de los polinomios de regresión. La primera característica identificada fue el orden del polinomio de retardo (nk) para cada curva de cambio de color respecto a cada una de las señales de volumen periférico (con y sin oclusión), de este modo se obtuvieron seis relaciones de retardo, dos por cada componente de color. La Tabla 1 presenta los resultados de cada nk asociado a cada relación salida-entrada existente en el modelo computacional.

Tabla 1. Órdenes de retardo nk para cada relación salida-entrada del modelo computacional
SalidaEntradank
Curva de cambio de color RojoVolumen periférico sin oclusión: Vmc30
Volumen periférico con oclusión: Vmo12
Curva de cambio de color VerdeVolumen periférico sin oclusión: Vmc6
Volumen periférico con oclusión: Vmo23
Curva de cambio de color AzulVolumen periférico sin oclusión: Vmc14
Volumen periférico con oclusión: Vmo15

De acuerdo a la ecuación (6) y (7), los polinomios A(q), B(q) y F(q) que representan la regresión de la salida y las entradas en los modelos lineales ARX y OE, tienen asociado órdenes na, nb y nf, que fueron calculados experimentalmente mediante el criterio AIC según la ecuación (8) y que representan de la mejor manera la dinámica de las curvas de cambio color, esto fue medido a través del porcentaje de ajuste FIT (ecuación (9)). La Tabla 2 muestra los mejores órdenes obtenidos para dichos polinomios.

Tabla 2. Órdenes de los polinomios que representan cada relación salida-entrada de los modelos lineales
SalidaEstructura linealnanb (Vmc)nb (Vmo)nf (Vmc)nf (Vmo)
Curva de cambio de color RojoARX1615------
OE--- 22
Curva de cambio de color VerdeARX1412------
OE--- 12
Curva de cambio de color AzulARX1615------
OE--- 21

[i] * El modelo ARX no presenta polinomio F(q) mientras que el modelo OE no presenta polinomio A(q). Por tanto, se presenta la celda en gris.

La Figura 2 presenta los resultados luego de la predicción de la salida a través de los modelos computacionales identificados ARX y OE, para cada componente de color rojo, verde y azul. La línea negra representa la curva de cambio de color real tomada para diseñar cada modelo. Para cada curva de cambio de color se definió un modelo de identificación diferente. La línea amarilla es el resultado que predice el modelo con estructura ARX, el porcentaje de ajuste FIT fue de 83,3%, 73%, 65,6% para rojo, verde y azul respectivamente. La línea cian es el resultado de predicción para la estructura lineal OE, con valores de FIT de 92,2%, 89,2% y 90,4% para cada espacio de color. Los polinomios que definen esta última estructura fueron usados como elemento lineal del arreglo HW, ya que este presentó los mejores porcentajes de ajuste.

Figura 2. Salida de los sistemas identificados con ARX, OE y HW para cada componente de color: (A) Rojo, (B) Verde y (C) Azul
0124-7107-reus-20-02-00139-gf2.png

La estructura de identificación no lineal HW, cuyo resultado de predicción se presenta con el trazo fucsia en la Figura 2, presentó porcentajes de ajuste de 94,6%, 96,9% y 95,6%, respectivamente. El modelo HW está compuesto por bloques en cascada, uno representa una estructura de tipo lineal y está dado por los mejores órdenes nb y nf de la estructura OE reportados en la Tabla 2. El bloque no lineal está representado por una función estática que permite establecer cada relación existente en el bloque lineal. Los mejores resultados de FIT se obtuvieron para entradas representadas con una función sigmoidea y salidas representadas por una función lineal descrita a tramos.

Discusión

Los volúmenes obtenidos con y sin oclusión representan en buena forma la dinámica de la vasculatura periférica. El cambio realizado en la simulación del brazalete de oclusión del modelo de Goldoozian et al.15, permitió representar los cambios que sufre el volumen sanguíneo frente al estímulo isquémico, y por ende es una buena aproximación de entrada al sistema de identificación computacional.

La Figura 2 presenta los porcentajes de ajuste (FIT) para cada modelo de identificación computacional. El modelo lineal ARX es el que presenta el menor ajuste en la predicción de las curvas de cambio de color, mientras que el modelo OE presenta mayor bondad de predicción. Es por esto que se usó el modelo OE como componente lineal de la estructura HW, que, si bien el modelo OE presenta un porcentaje de ajuste elevado para los cambios de color de los tres espacios, el modelo no lineal representa finalmente mejores resultados en cuanto al ajuste de la morfología de la curva y la dinámica del sistema, esto es debido a que las curvas de cambio de color tienen una forma no convencional y los modelos lineales fallan al tratar de simular grandes inflexiones y concavidades en las curvas.

Si bien, en este artículo se ha propuesto un modelo no lineal para representar la relación entre los volúmenes de perfusión y los cambios de color que se presentan en las manos durante la hiperemia reactiva en uno de los brazos, es posible reemplazar la segunda etapa del modelo por uno que represente la técnica diagnóstica de interés, por ejemplo, para validar técnicas basadas en la morfología de la onda de presión, como lo hace el sistema Arteriograph27 o los cambios en el diámetro arterial medidos a partir de la dilatación mediada por flujo (FMD).

Para cada técnica diagnóstica se obtendría un modelo representativo en la segunda etapa y dichos modelos resultarán de utilidad para comparar técnicas diagnósticas al identificar grupos de sujetos sanos jóvenes, mayores o enfermos, entre otros.

Una de las limitaciones de la presente investigación es que se ha asumido que la dinámica vascular es lineal, por ello, se propone modificar la primera etapa del modelo, de esta manera contemplar el mecanismo de regulación hemodinámica a lo largo de la arteria, conocido como autoregulación, donde se tendrían presentes parámetros metabólicos que afectan la circulación sanguínea y se modelarían los cambios de vasodilatación y vasoconstricción. Otra de las limitaciones del modelo es que los resultados de predicción obtenidos aún no han sido contrastados respecto al Gold Standard de estimación de RV, por esto, se proponen pruebas en trabajos futuros. Además, debido a que sólo se usaron los datos de un sujeto sano para el desarrollo del modelo de identificación, se propone realizar el ajuste del modelo en una población de sujetos que esté compuesta por sujetos sanos, pacientes con riesgo cardiovascular y pacientes crónicos.

Fuentes de financiación

Este trabajo ha sido financiado por el Sistema General de Regalías, República de Colombia a través del proyecto "Fortalecimiento de la plataforma tecnológica para la formación especializada en el área de la salud y el desarrollo de tecnología biomédica", código RutaN-139C.

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.

Referencias

1. World Health Organization. Global Status Report on Noncommunicable Diseases 2014. Ginebra: WHO; 2014. Disponible en: http://www.who.int/en/

2. Arrebola-Moreno AL, Laclaustra M, Kaski JC. Noninvasive Assessment of Endothelial Function in Clinical Practice. Rev Española Cardiol (English Ed. 2012;65(1):80-90. doi:http://dx.doi.org/10.1016/j.rec.2011.10.004.

3. Verma S, Anderson TJ. Fundamentals of endothelial function for the clinical cardiologist. Circulation. 2002;105(5):546-549. doi:10.1161/hc0502.104540.

4. Dhindsa M, Sommerlad SM, DeVan AE, et al. Interrelationships among noninvasive measures of postischemic macro- and microvascular reactivity. J Appl Physiol. 2008;105(2):427-432. doi:10.1152/japplphysiol.90431.2008.

5. McQuilkin GL, Panthagani D, Metcalfe RW, et al. Digital thermal monitoring (DTM) of vascular reactivity closely correlates with Doppler flow velocity. Conf Proc IEEE Eng Med Biol Soc. 2009;2009:1100-3. doi:10.1109/IEMBS.2009.5333962.

6. Takase B, Hamabe A, Satomura K, et al. Comparable Prognostic Value of Vasodilator Response to Acetylcholine in Brachial and Coronary Arteriesfor Predicting Long-Term Cardiovascular Events in Suspected Coronary Artery Disease. Circ J. 2006;70:49-76.

7. Corretti MC, Anderson TJ, Benjamin EJ, et al. Guidelines for the ultrasound assessment of endothelial-dependent flow-mediated vasodilation of the brachial artery: A report of the international brachial artery reactivity task force. J Am Coll Cardiol. 2002;39(2):257-265. doi:10.1016/S0735-1097(01)01746-6.

8. Budoff M, Ahmadi N, Kleis S, et al. Digital (Fingertip) Thermal Monitoring of Vascular Function: A Novel, Noninvasive, Nonimaging Test to Improve Traditional Cardiovascular Risk Assessment and Monitoring of Response to Treatments. In: Media SS, ed. Asymptomatic Atherosclerosis: Pathophysiology, Detection and Treatment. ; 2010:248-263.

9. Schier R, Marcus HE, Mansur E, et al. Evaluation of Digital Thermal Monitoring as a Tool to Assess Perioperative Vascular Reactivity. J Atheroscler Thromb. 2013;20(3):277-286.

10. Schier R, Schick V, Amsbaugh A, et al. Brachial artery reactivity and vascular reactive hyperemia for preoperative anaesthesia risk assessment -- an observational study. BMC Anesthesiol. 2014;14(1):1-10. doi:10.1186/1471-2253-14-47.

11. Zhang HD, He Y, Wang X, Shao HW, Mu LZ, Zhang J. Dynamic infrared imaging for analysis of fingertip temperature after cold water stimulation and neurothermal modeling study. Comput Biol Med Elsevier. 2010;40(7):650-656.

12. Wang X, He Y. Experimental Study of Vascular Reactivity in the Fingertip: An Infrared Thermography Method. Biomed Eng Informatics (BMEI), 2010 3rd Int Conf. 2010;3:1180-1184. doi:10.1109/BMEI.2010.5639589.

13. Zahedi E, Jaafar R, Mohd Ali MA, Mohamed AL, Maskon O. Finger photoplethysmogram pulse amplitude changes induced by flow-mediated dilation. Physiol Meas. 2008;29(5):625-637. doi:10.1088/0967-3334/29/5/008.

14. Selvaraj N, Jaryal AK, Santhosh J, Anand S, Deepak KK. Monitoring of reactive hyperemia using photoplethysmographic pulse amplitude and transit time. J Clin Monit Comput. 2009;23(5):315-322. doi:10.1007/s10877-009-9199-3.

15. Goldoozian LS, Zahedi E. Electrical analog model of arterial compliance during reactive hyperemia. Biomed Eng (MECBME), 2011 1st Middle East Conf. 2011:49-53. doi:10.1109/MECBME.2011.5752062.

16. Lanzarone E, Liani P, Baselli G, Costantino ML. Model of arterial tree and peripheral control for the study of physiological and assisted circulation. Med Eng Phys. 2007;29(5):542-555. doi:10.1016/j.medengphy.2006.08.004.

17. Lanzarone E, Casagrande G, Fumero R, Costantino ML. Integrated model of endothelial no regulation and systemic circulation for the comparison between pulsatile and continuous perfusion. IEEE Trans Biomed Eng. 2009;56(5):1331-1340. doi:10.1109/TBME.2009.2014738.

18. Westerhof N, Bosman F, De Vries CJ, Noordergraaf A. Analog studies of the human systemic arterial tree. J Biomech. 1969;2(2):121-143.

19. Mashayekhi G, Zahedi E. Modeling blood flow & pressure in systemic circulation with cuff occlusion. Biomed Eng (ICBME), 2013 20th Iran Conf. 2013:48-53. doi:10.1109/ICBME.2013.6782191.

20. Babbs CF. Oscillometric measurement of systolic and diastolic blood pressures validated in a physiologic mathematical model. Biomed Eng Online. 2012;11(1):56. doi:10.1186/1475-925X-11-56.

21. Barrebet KE, Barman SM, Boitano S, Brooks HL. Ganong, Fisiología Médica. 23a ed. México: McGraw-Hill; 2010.

22. Kendall M. Rank Correlation Methods. United States: Charles Griffin and Company; 1962.

23. Ljung L. System identification - Theory for the User. United States: Prentice Hall. 1999.

24. Akaike H. A New Look at the Statistical Model Identification. IEEE Trans Automat Contr. 1974;19(6):716-723. doi:10.1109/TAC.1974.1100705.

25. Dolanc G, Strmcnik S. Identification of nonlinear systems using a piecewise-linear Hammerstein model. Syst Control Lett. 2005;54(2):145-158. doi:10.1016/j.sysconle.2004.08.002.

26. Lusson Cervantes A, Agamennoni OE, Figueroa JL. Use of Wiener Nonlinear MPC to control a CSTR with multiple steady state. Lat Am Appl Res. 2003;33(2):149-154.

27. Lenkey Z, Illyés M, Böcskei R, et al. Comparison of arterial stiffness parameters in patients with coronary artery disease and diabetes mellitus using Arteriograph. Physiol Res. 2014;63(4):429-437.

Notes

Arboleda-Gómez DC, Aristizábal-Nieto JK, Hernández-Valdivieso AM. Modelado del sistema cardiovascular para evaluación de técnicas de estimación de reactividad vascular basadas en hiperemia reactiva. Univ. Salud. 2018;20(2):139-148. DOI: http://dx.doi.org/10.22267/rus.182002.118